试图做些笔记
printf("Hello");
What’s Machine Learning
A computer program is said to learn from experience E with respect to some task T and some performance measure P,if its performance on T,as measured by P,improves with experience E.
一些符号(?)
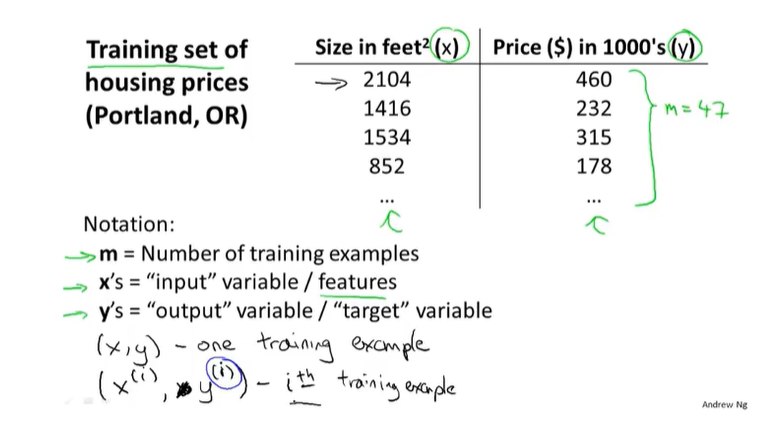
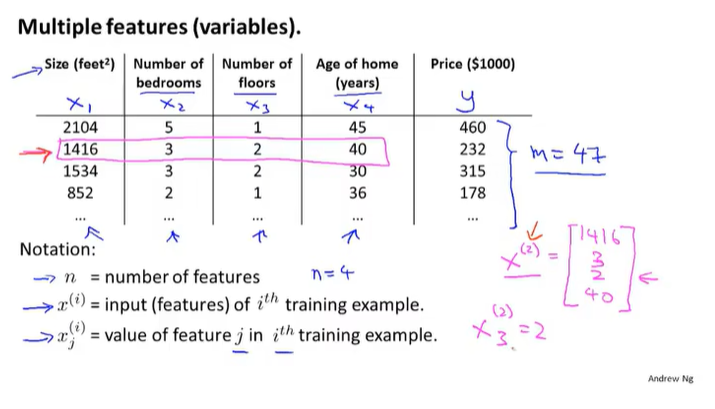
$(x^i,y^i)$表示第i个数据集,即表格中第i行
大写字母如A,B,X,Y表示矩阵,小写字母如a,b,x,y表示向量
监督学习
1.定义
大致定义
给予机器一些正确答案(即数据集),让机器推测出更多的正确答案
eg.给不同平方的房子的价格,让机器人推测出任意面积大小房子的价格
具体定义
1.Regression(回归问题):
Predict continuous valued output(price)
设法预测连续值的属性
2.Classification(分类问题):
Discrete valued output(in this example is 0 or 1)
设法预测一个离散值输出
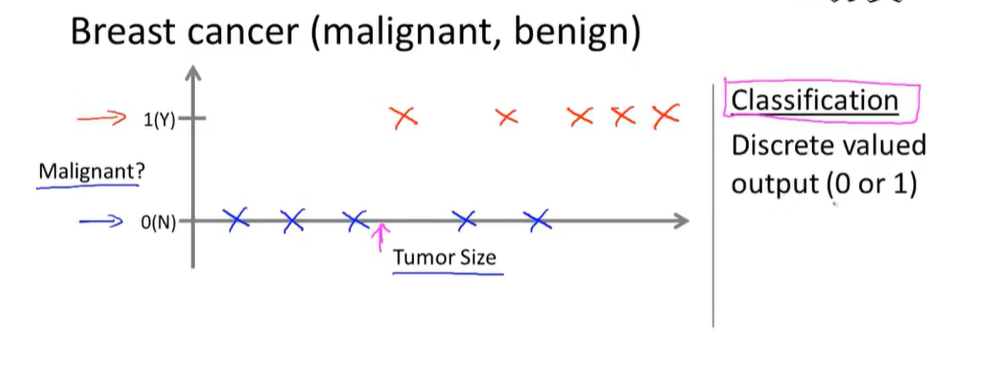
上图中仅有一个特征值,在实际应用中可能有多种特征值,forexample:
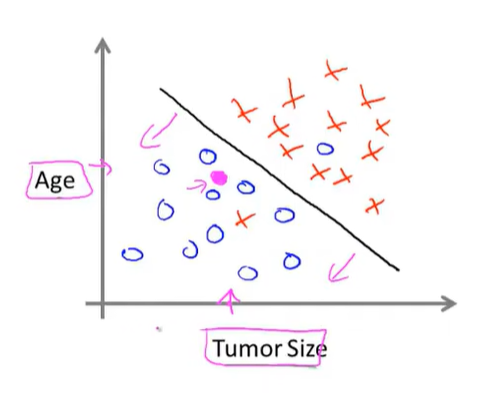
图中⚪表示良性肿瘤,×表示恶性肿瘤
当然还会有无穷多特征值的情况,等待后续学习。
2~7为连续型
2.单元线性回归模型
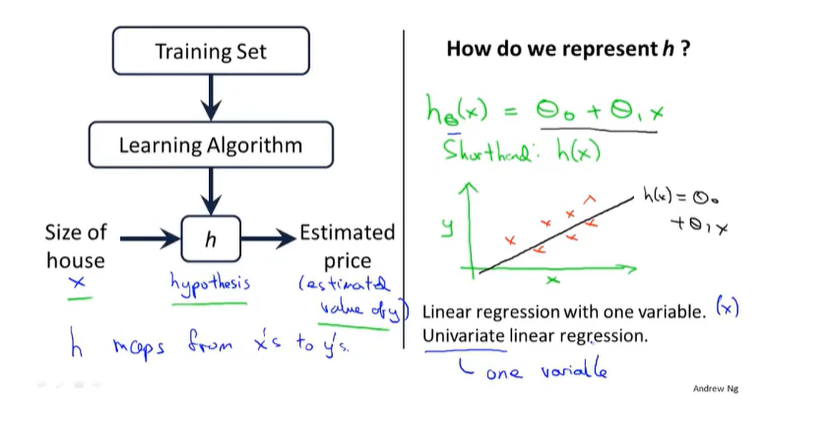
图中h指的是函数;$\theta_{0}$与$\theta_{1}$为参数,类似y=kx+b中的k与b;uniavariable意思为单变量的

目的是寻找使minimize后面那一串公式(懒得打了)的值最小的$\theta_{0}$与$\theta_{1}$,引入J($\theta_{0}$,$\theta_{1}$),即代价函数,该种代价函数也被称为平方误差(代价)函数,为解决回归问题最常用的手段
1.平方误差代价函数相关
当h中$\theta_{1}=0$时得到的J($\theta_{0}$,$\theta_{1}$)与$\theta_{0}$的图像为抛物线,当$\theta_{1}\not=0$时得到的3D图像如下所示
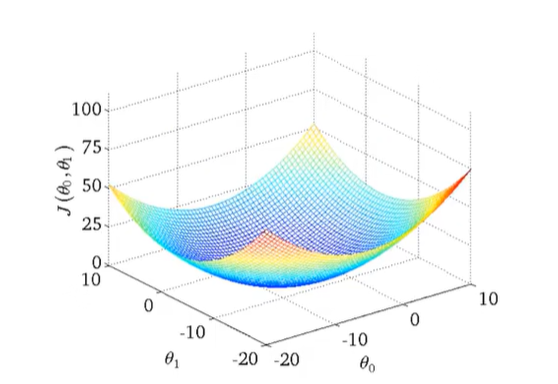
采用等高线(即在同一密闭曲线上的J值相等)得到的图像如下所示(地理中的盆地(雾))
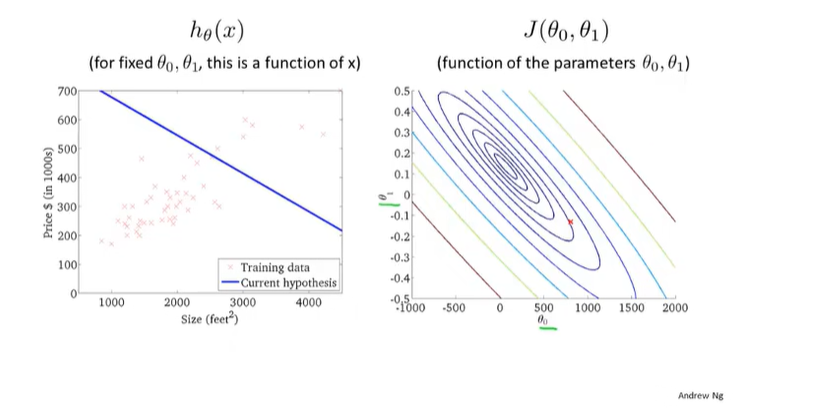
2.梯度下降算法
问题描述

直观表示就是随机从一个点出发,寻找周围梯度最小的方向,往前走一步,然后再寻找梯度最小的方向,不断重复以上过程
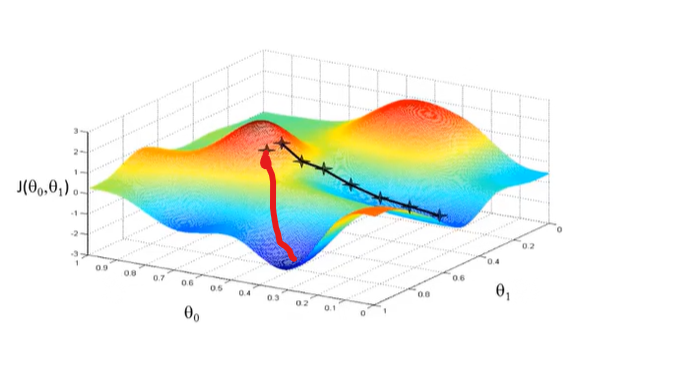
如图中所示,如果从不同的点出发会到不同的局部最优解
接下来是数学过程(没想到在这也能遇到微积分 sad)

右边为错误算法,两个参数应同时更新
图中:=为赋值运算符
如果说a:=b,则是将b的值赋给a
如果说a=b,则是判定a是否等于b,即a==b
$\alpha$被称为学习率,永远是正值,用来控制梯度下降时迈出多大的步子,$\alpha$越大表示梯度下降的速度越快,$\alpha$过小则收敛速度过慢,$\alpha$过大则可能导致无法收敛甚至发散
有关为什么是减偏导数
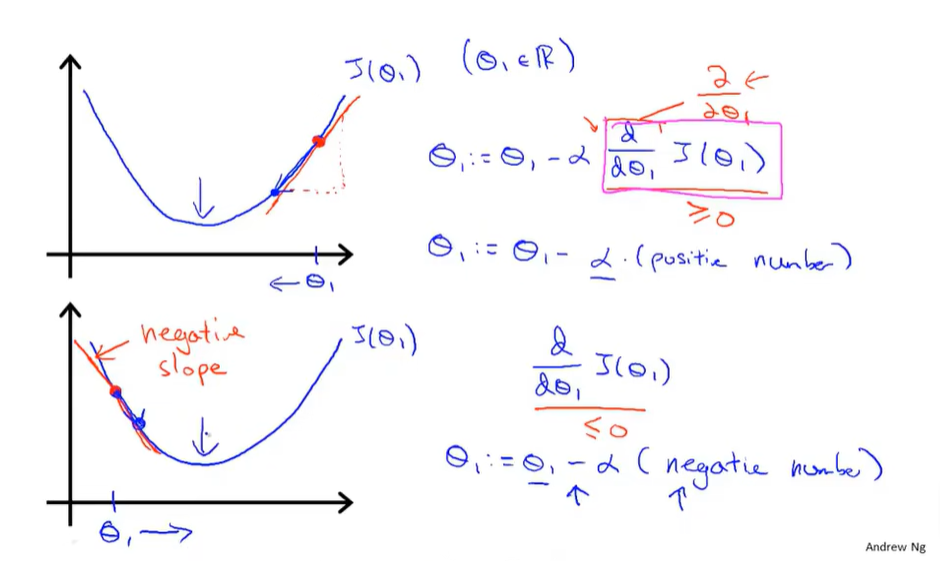
关于$\theta_{1}$到局部最优解时梯度下降法在干些啥
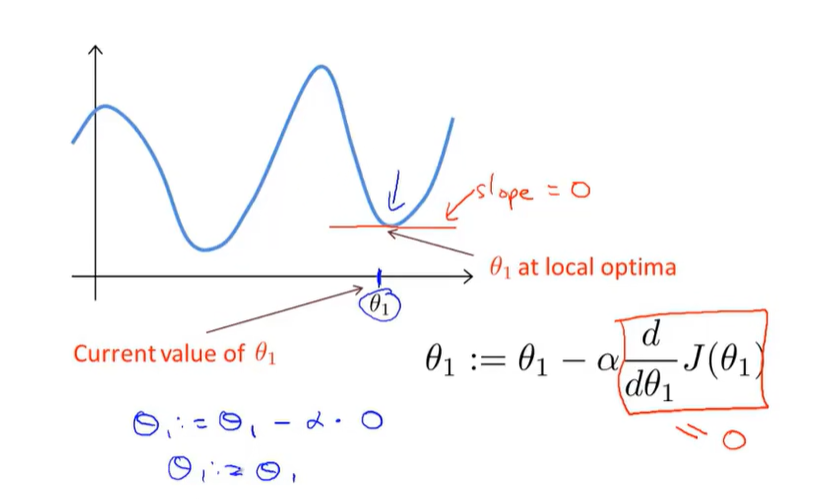
解释了为啥即使选取了合适的$\alpha$梯度下降也可能收敛到局部最优而不是全局最优
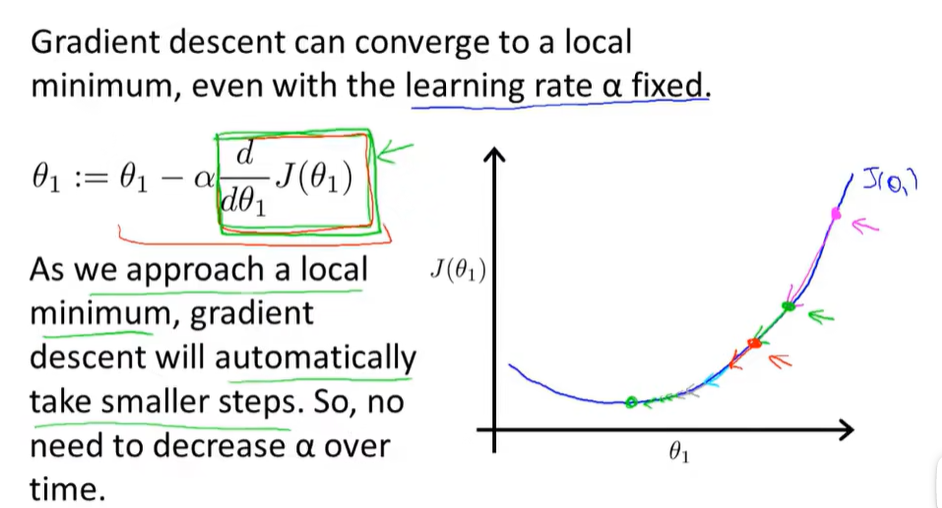
3.混~合~~到一起~

虽然可能有局部最优解问题的出现,但平方误差代价函数的图像是一个碗,所以不存在这个问题
将平方误差代价函数用梯度下降来求最优解的方法是Batch算法的一种,其定义为:Each step of gradient descent uses all the training examples(每一步梯度下降都历遍了整个训练集的样本),体现在该方法中为那个求和
3.多元线性回归模型


图中划掉部分表示可以用一个小写字母,即向量来表示它们整体

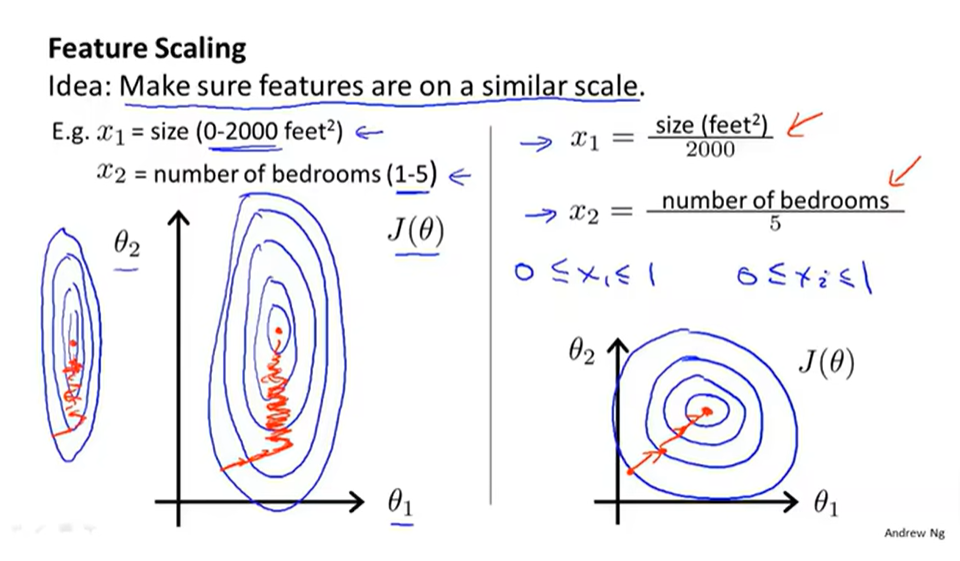
特征缩放
当不同特征值的取值范围相差很大时会导致代价函数的图象挤到一起,在采用梯度下降算法时会走很多崎岖的路,故此时需采用特征缩放


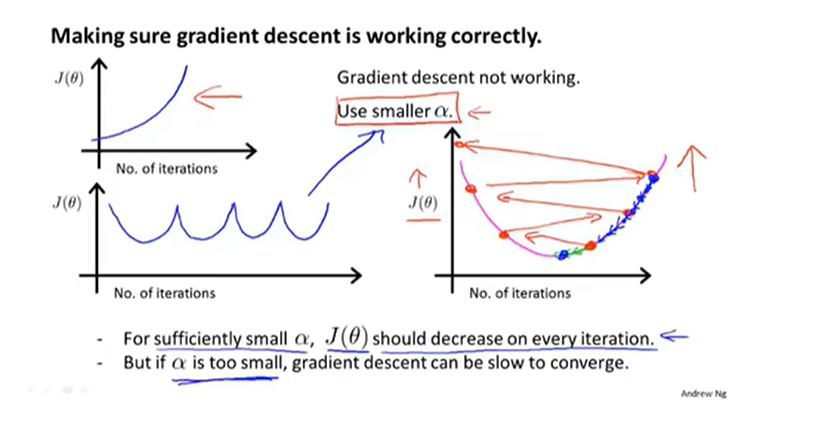
4.保证梯度下降在正常工作
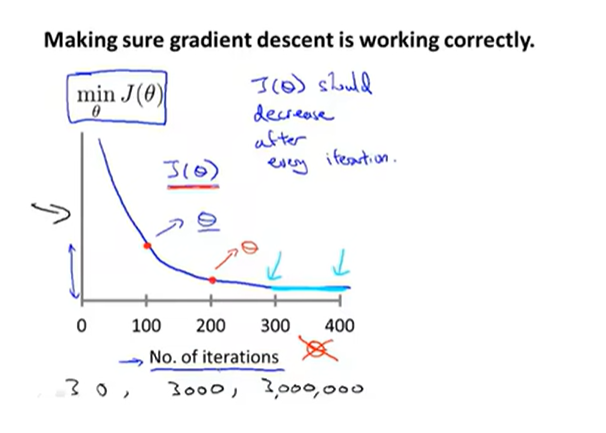
画出代价函数随迭代步数增加的变化曲线来判断梯度下降算法是否已经收敛
5.学习率的选择

6.线性回归模型中特征值的选择
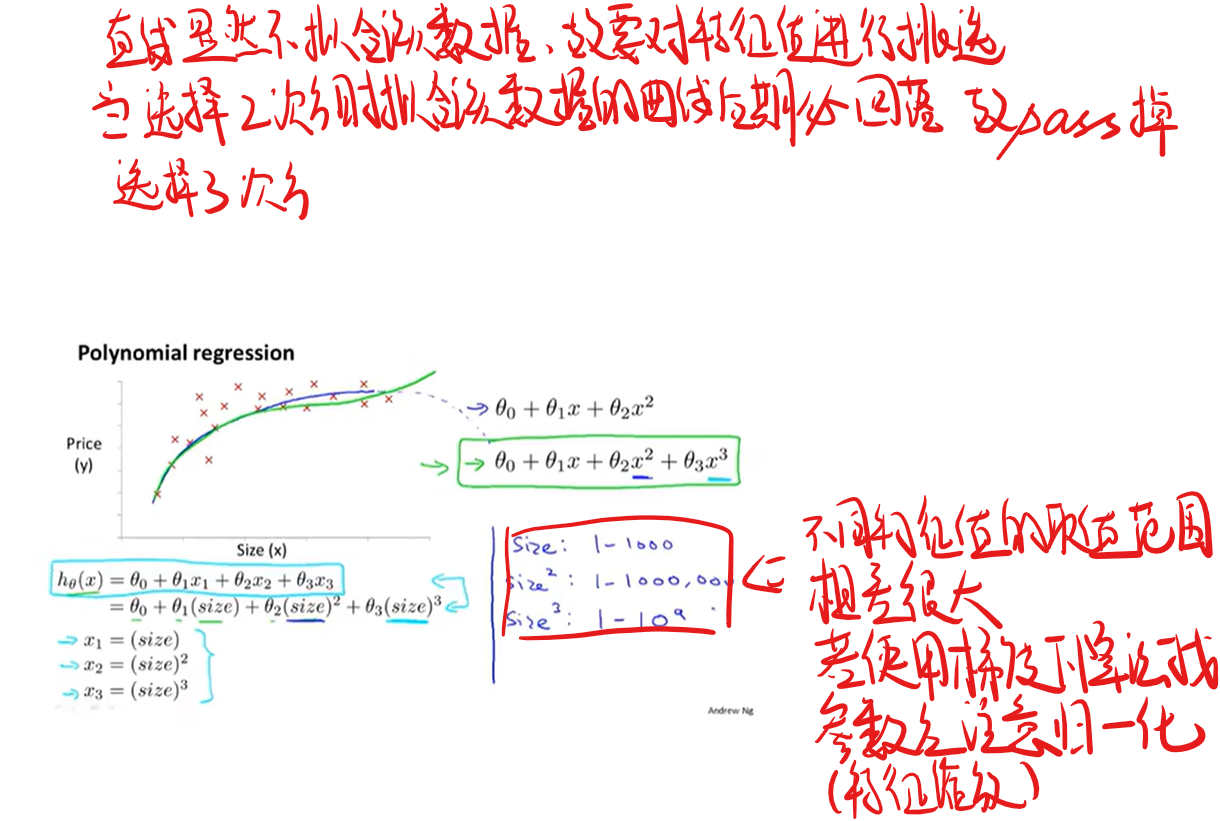
当然这不是唯一的一种选择,在该例子中还可选择开方,可以选多种特征值组合最后看哪个方案得到的代价函数最小
7.正规方程(比梯度下降更直接的方法)
最小二乘法(救命这是啥啊全忘了sos)
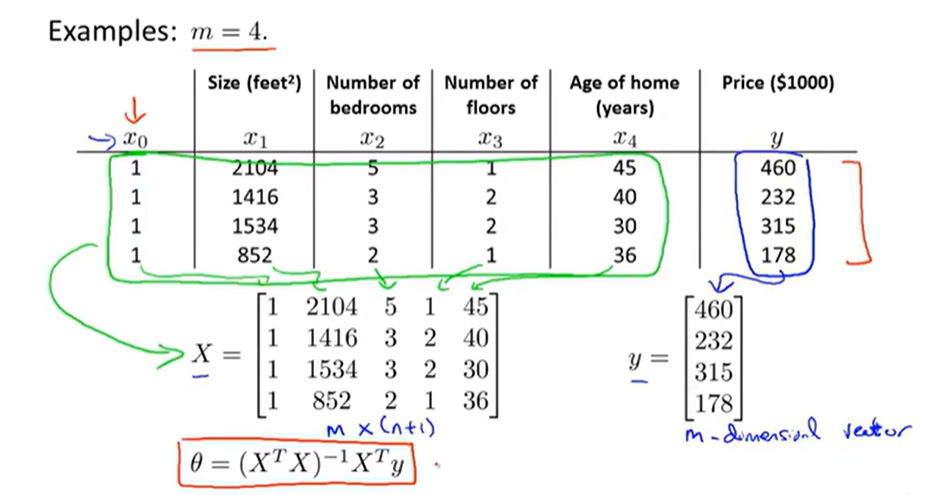
用正规方程法不用进行特征缩放

如果$X^TX$不可逆如何解决(貌似以下过程在编译过程中会自动完成)

8.分类问题

显然线性回归模型现在不太适用,引入新的算法Logistic Regression Model
Logistic Regression Model
1.对该模型的一些阐述
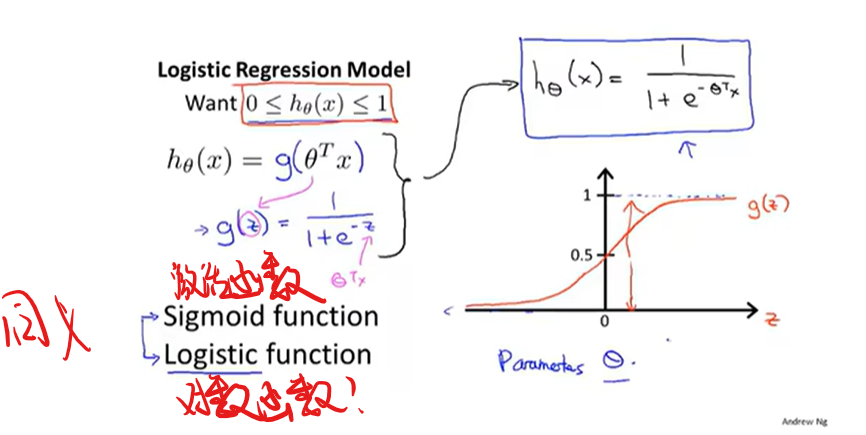

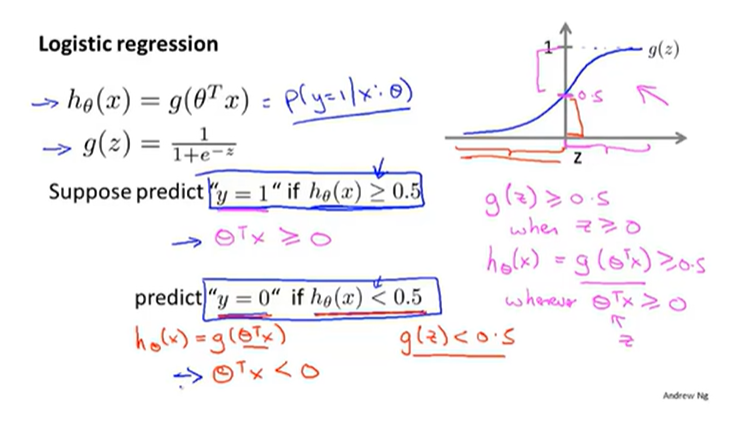

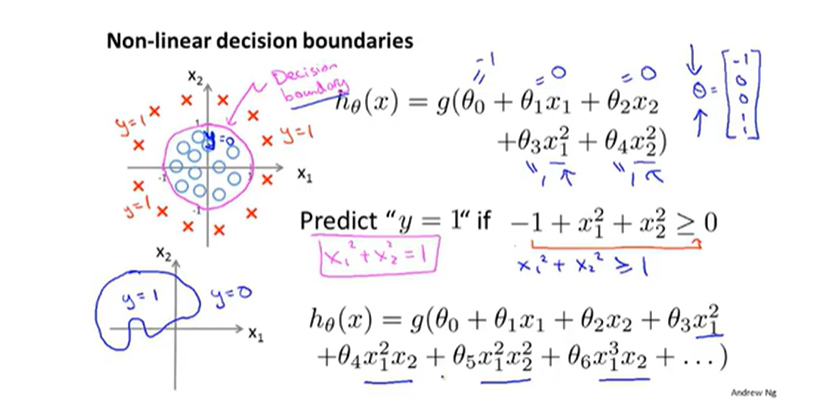
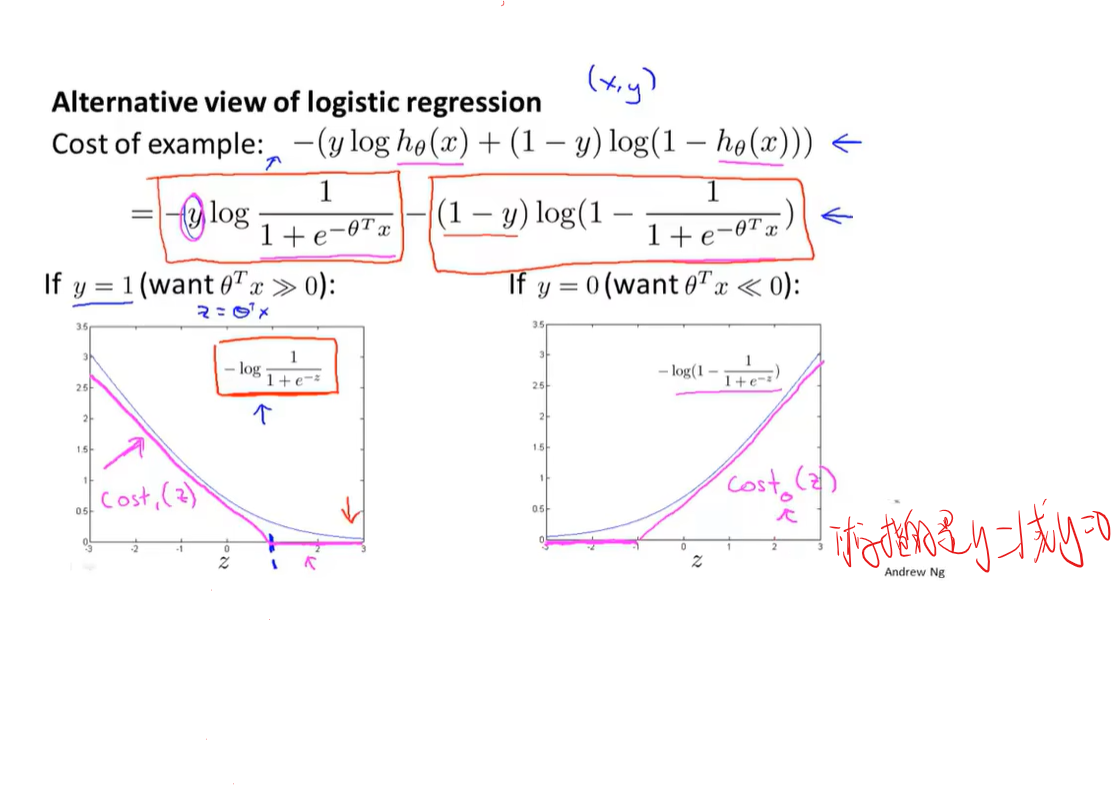
2.该模型使用的代价函数与取参数的多种算法
如果接着采用之前的平方误差代价函数会导致代价函数有许多局部最优解,所以更新换代了!换成如下的代价函数保证得到的是凸函数(弹幕里说这里凸函数和国内的定义是反的 但我根本不记得这玩意的定义是啥了)

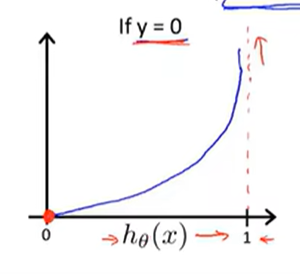
下面对代价函数进行简化



3.多元分类问题:一对多

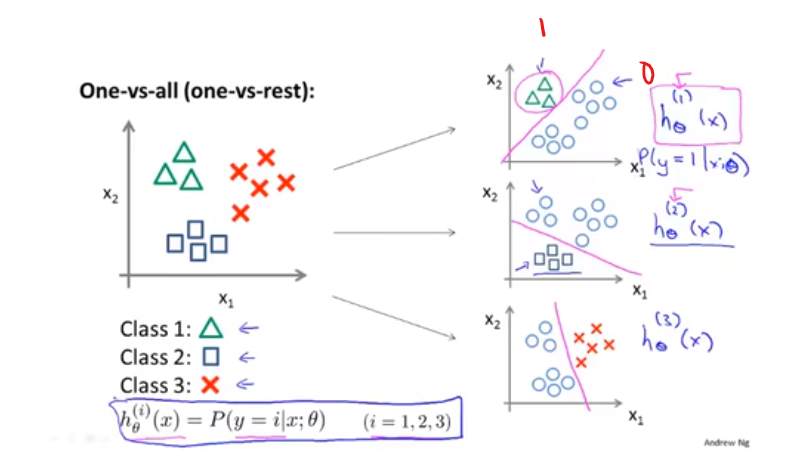

正则化相关
什么是过拟合和欠拟合
线性回归中
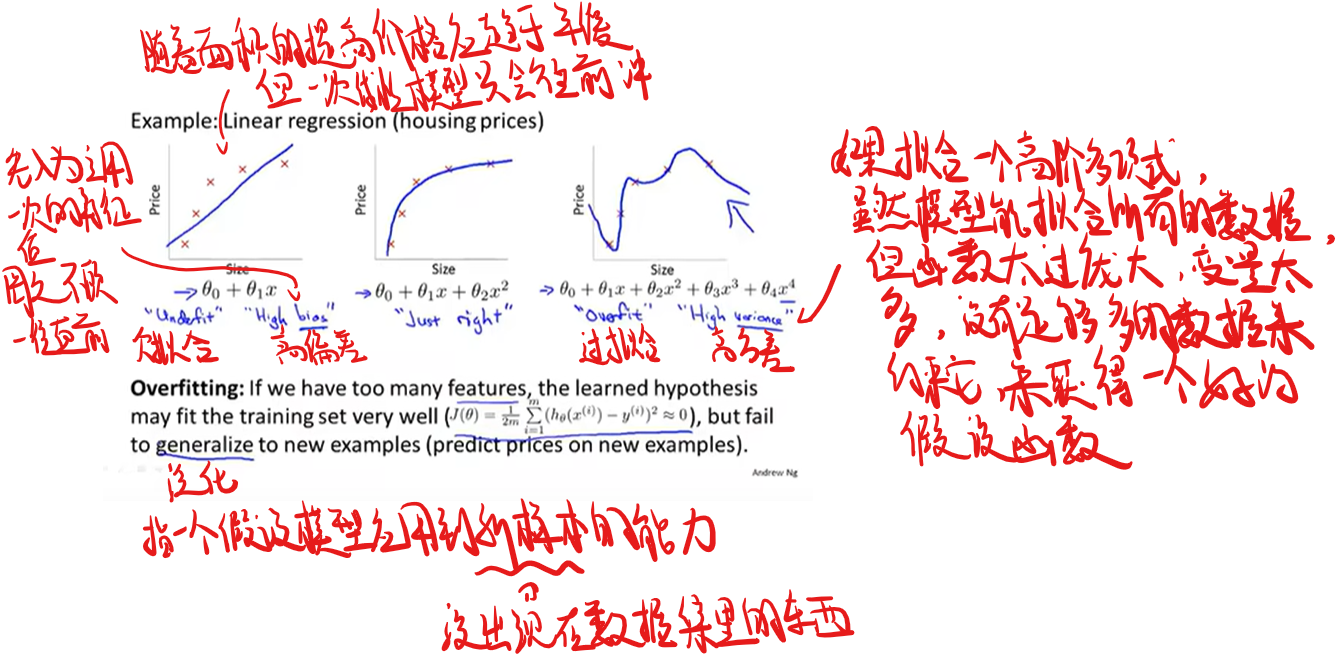
逻辑回归中
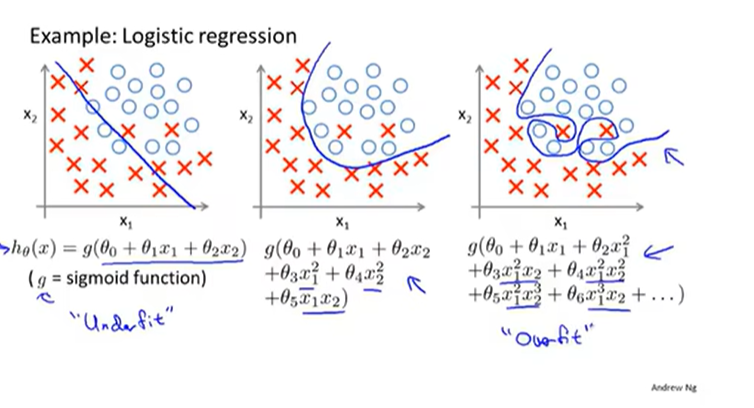
如何解决过拟合

代价函数中进行正则化

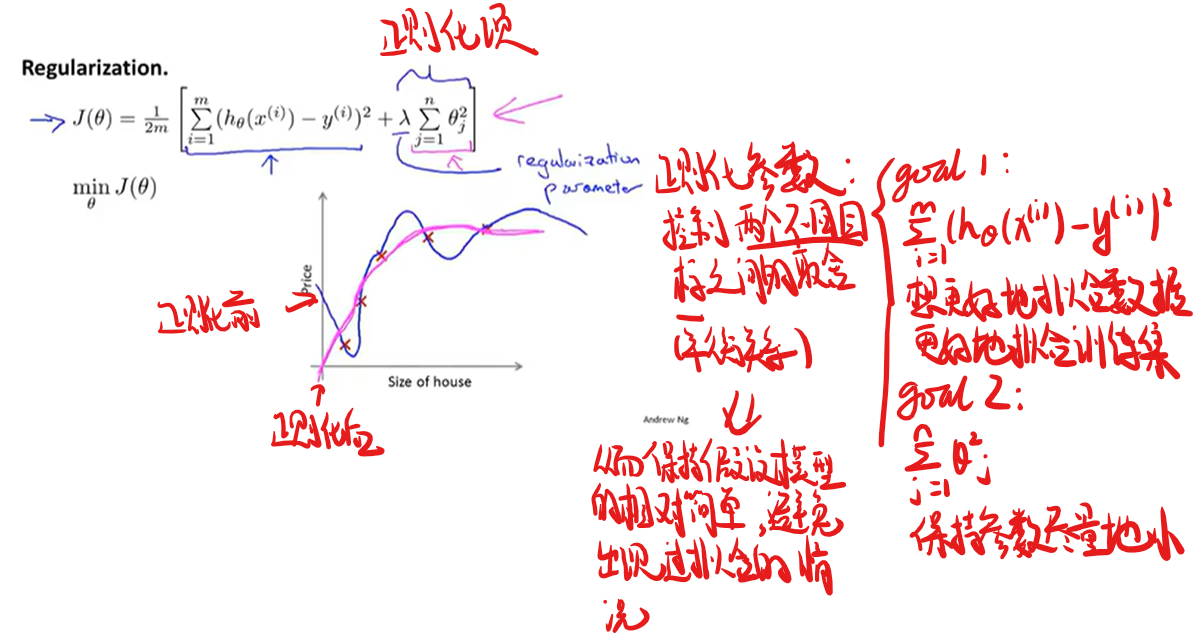

线性回归的正则化
梯度下降的

正规化方程的


Logistic回归的正则化


插播点东西


谢谢您 这就去退学去硅谷
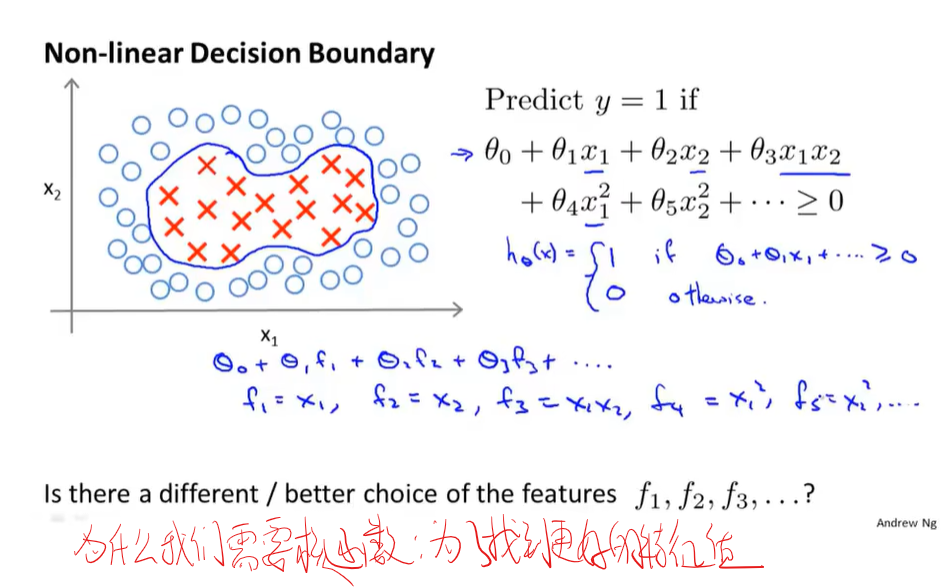
非线性假设
神经网络

神经元模型
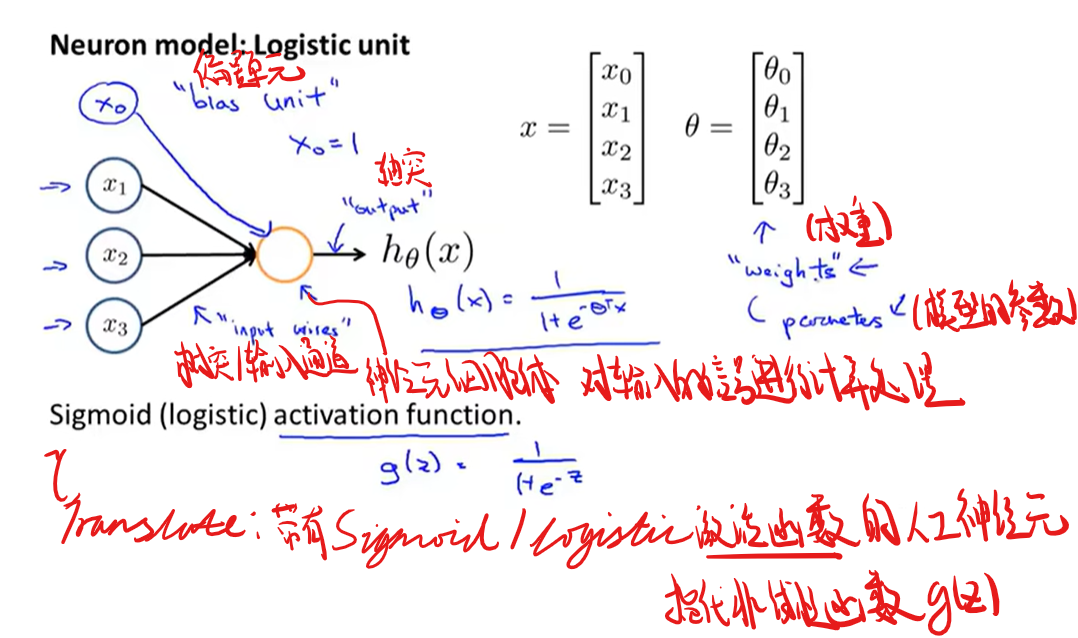
神经网络模型
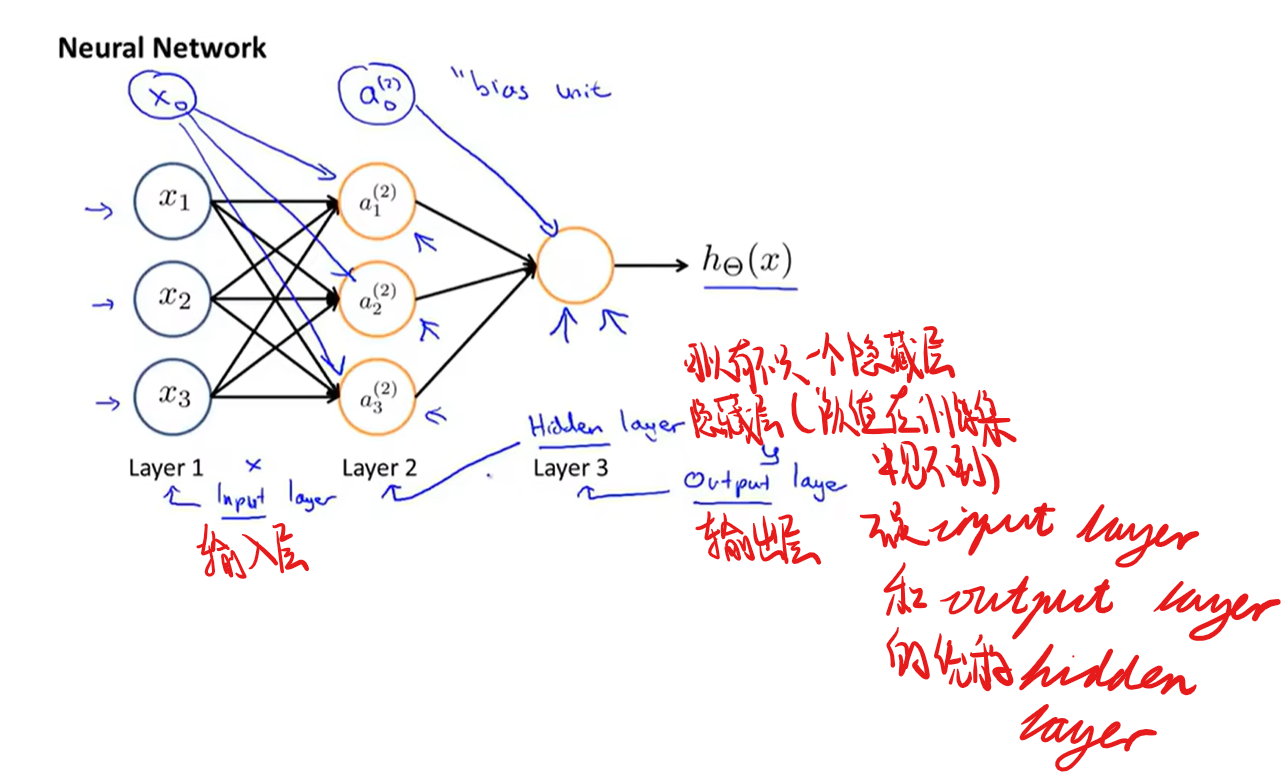
神经网络中的计算


这个神经网络所做的事就像是逻辑回归,但不是使用原先的$x_{1},x_{2},x_{3}$作为特征,而是用$a_{1}^{(2)},a_{2}^{(2)},a_{3}^{(2)}$作为新的特征值,这些是学习得到的函数输入值,具体来说,就是从第一层映射到第二层的函数,这个函数由其他参数$\theta^{(1)}$决定(相当于通过原始特征计算出更好的特征作为训练模型使用)
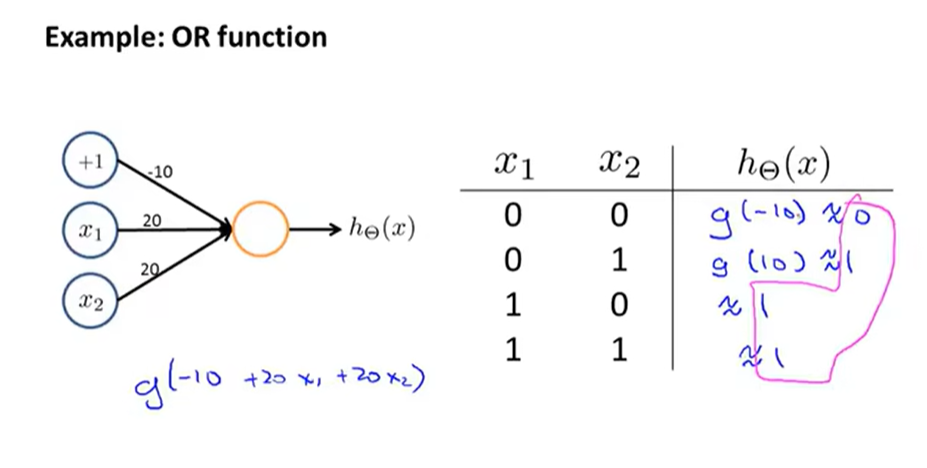
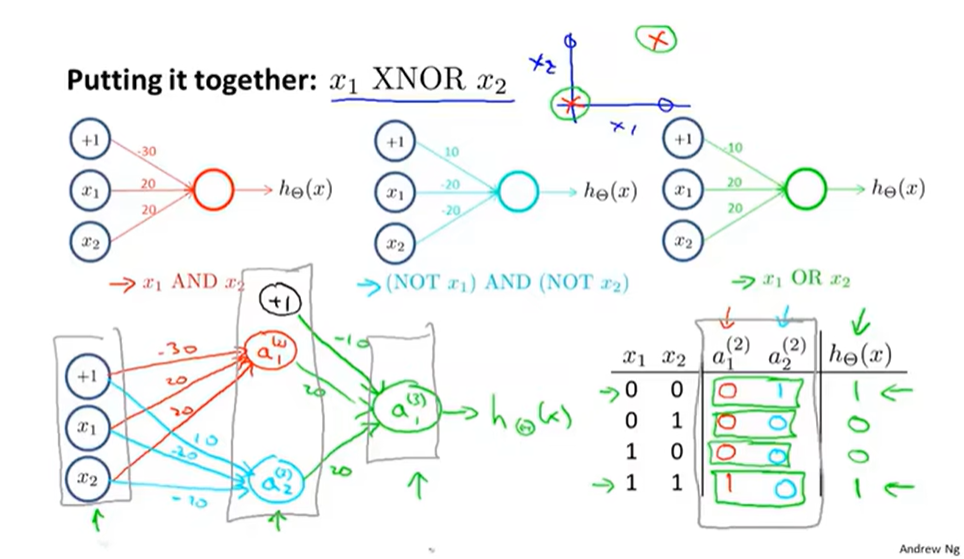
有关神经网络如何计算复杂非线性函数的输入的例子
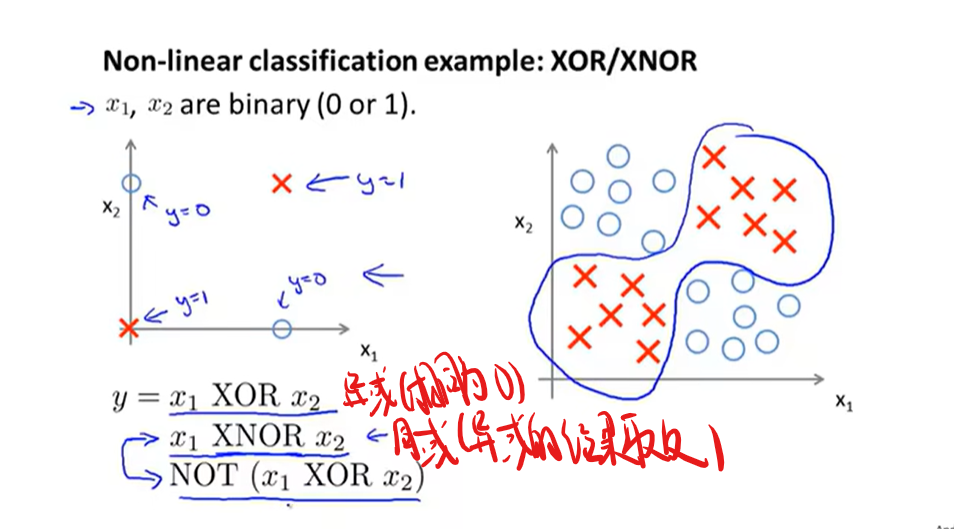
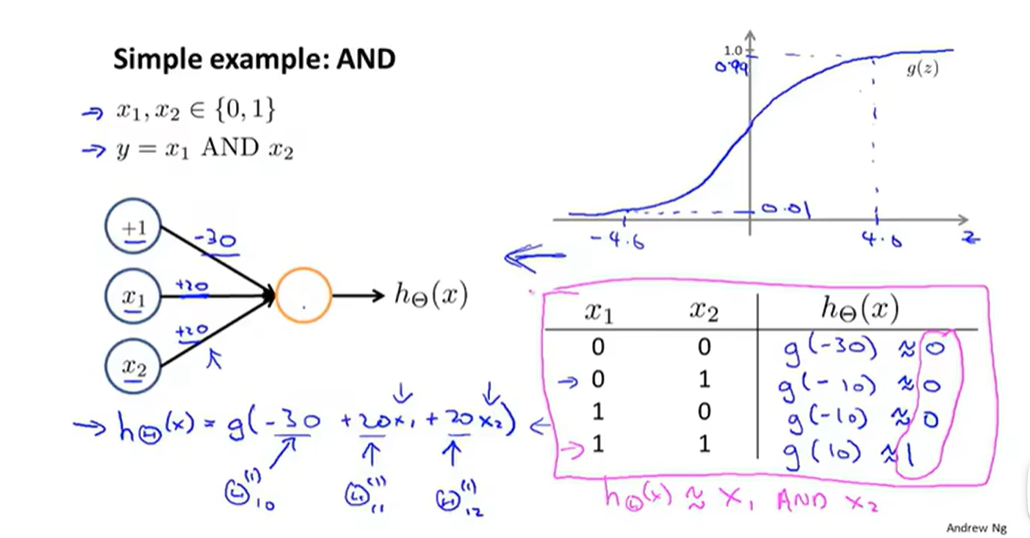
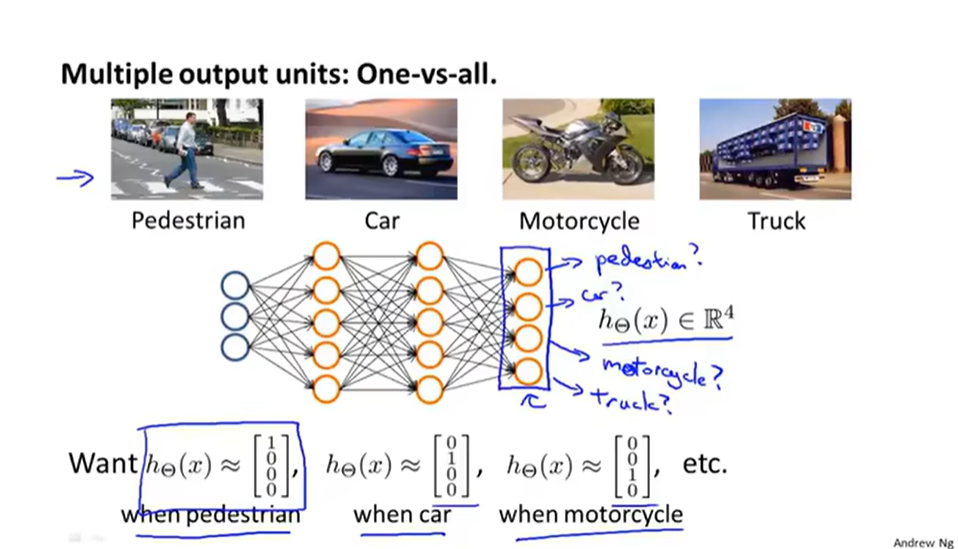
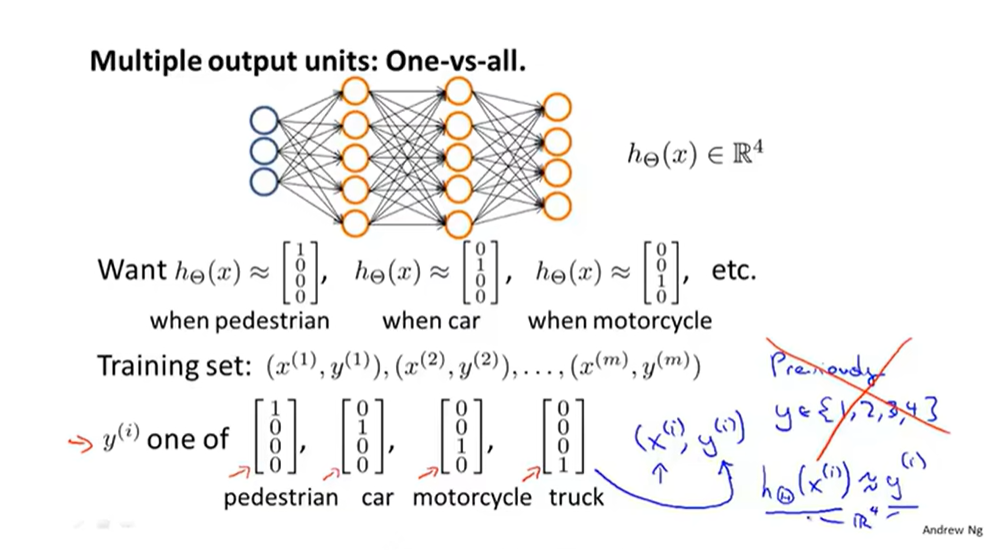
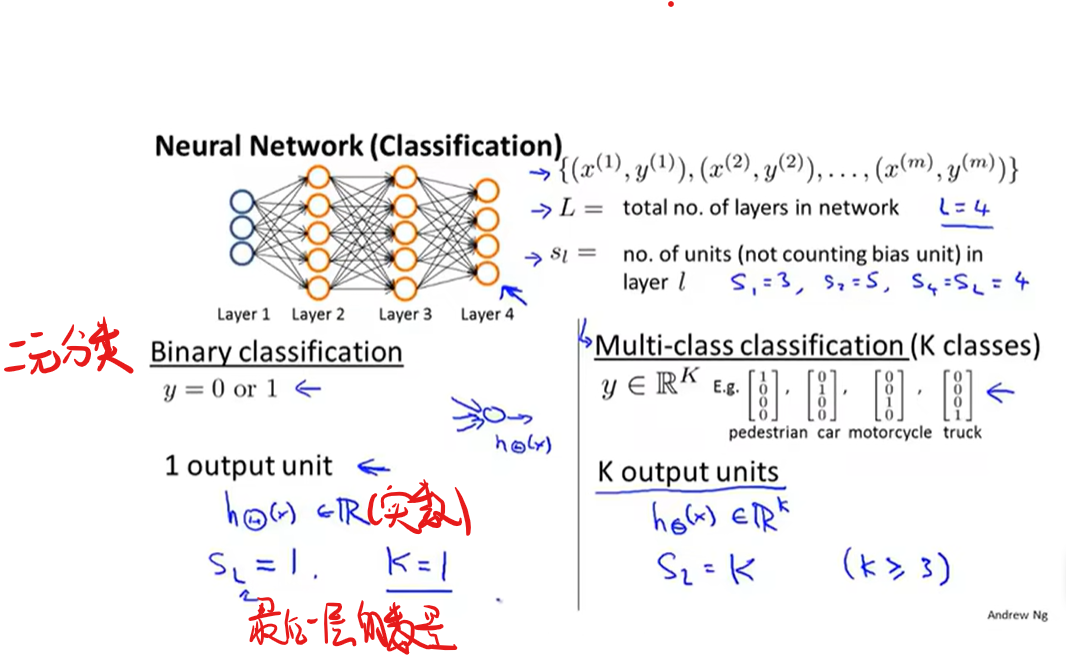
神经网络实现多元分类
神经网络中的代价函数
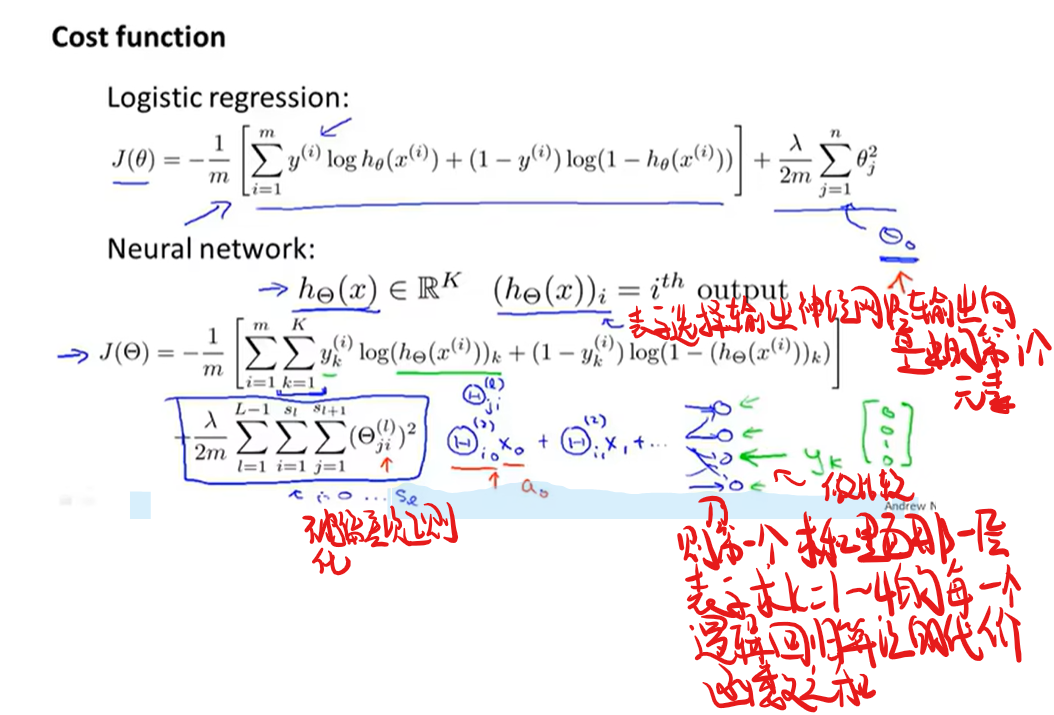
反向传播算法



试图理解反向传播
先复习一哈正向传播
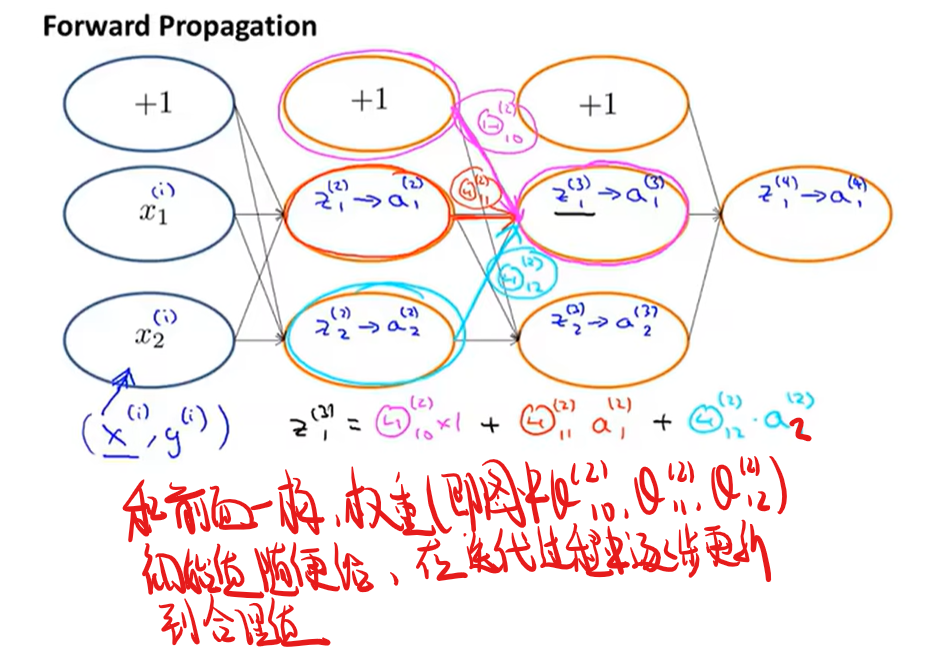

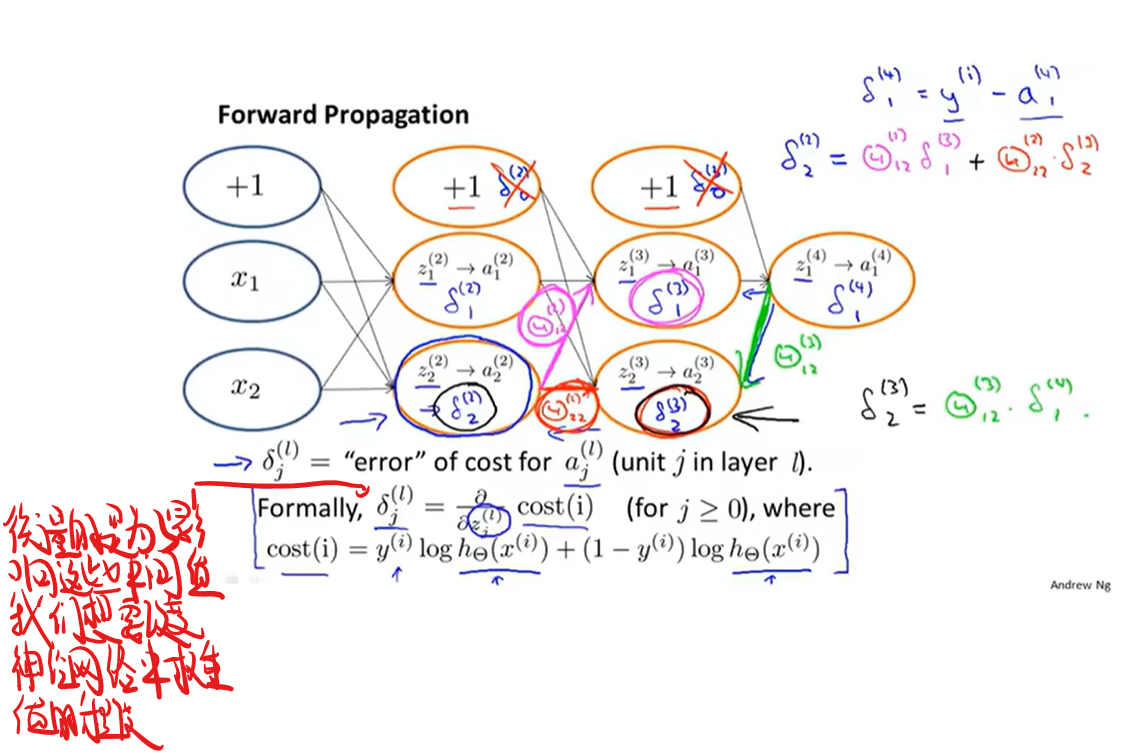
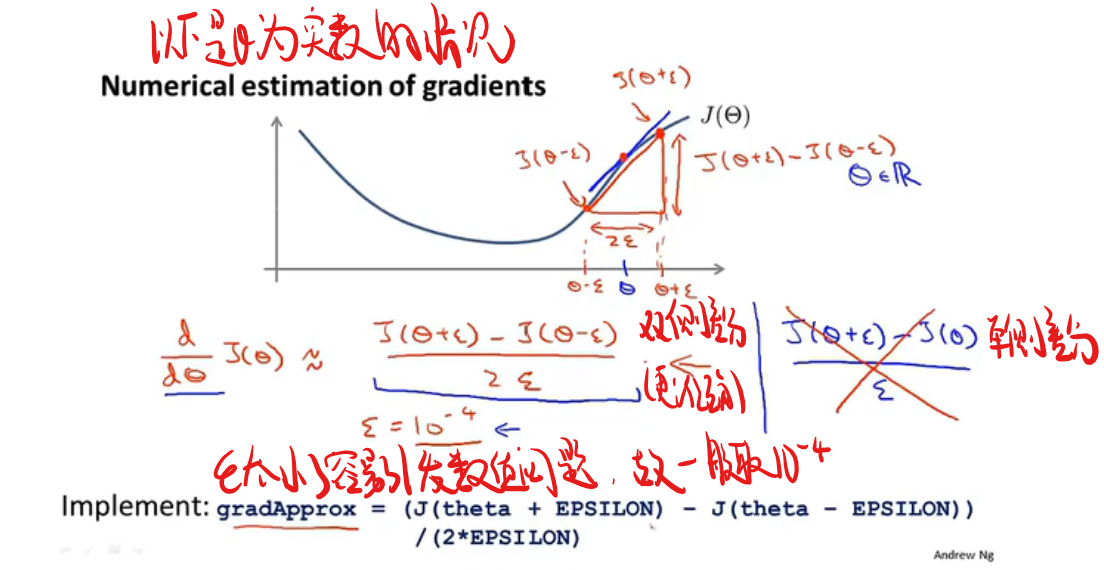
梯度检验
在反向传播的过程中很容易产生一些bug,但虽然有bug它的代价函数还是能不断减少,但最后得到的数据会比没有bug高一个量级,故需要一个东西来检验一下是否出现了bug,这就是(当当当当)梯度检验!(试图伪装出我热爱学习的样子)

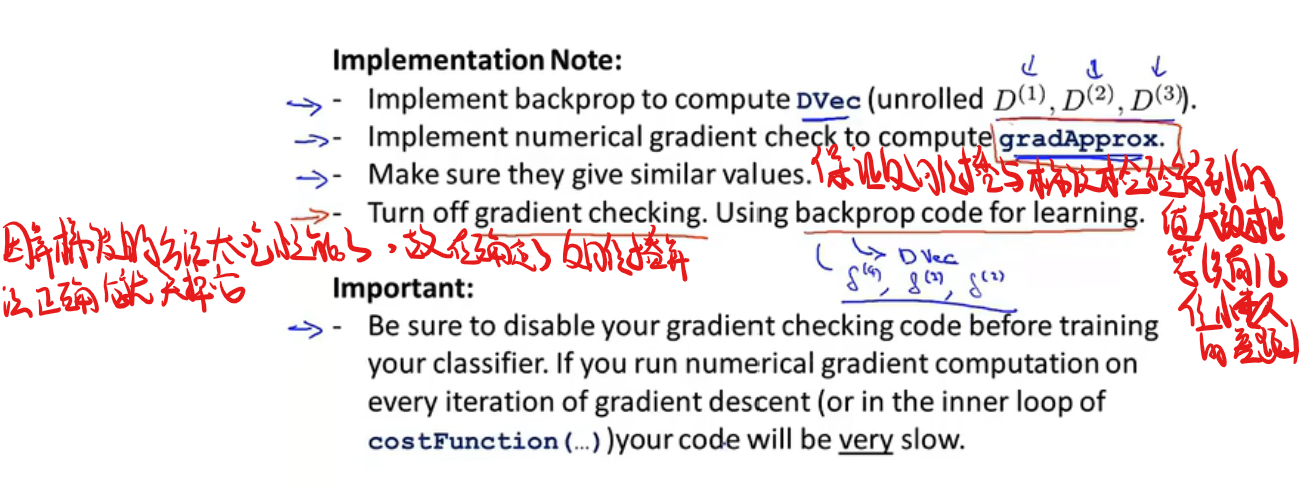
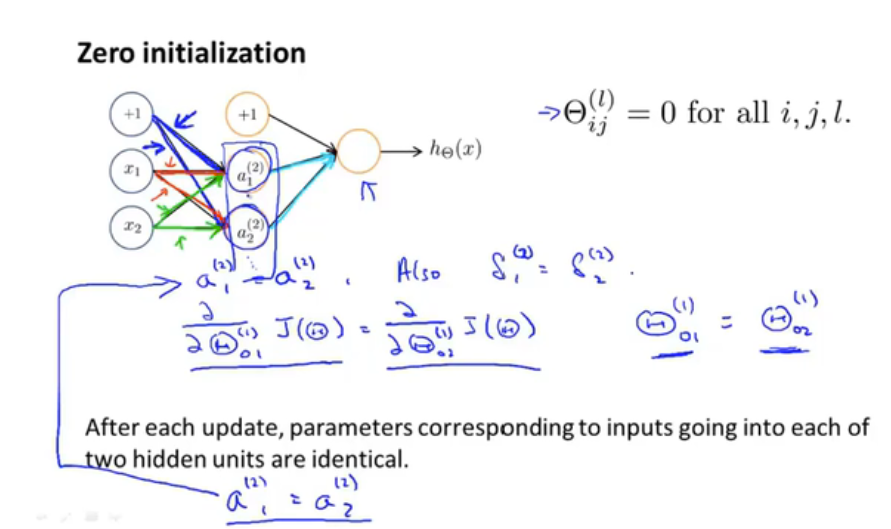
如何选取初始权重值

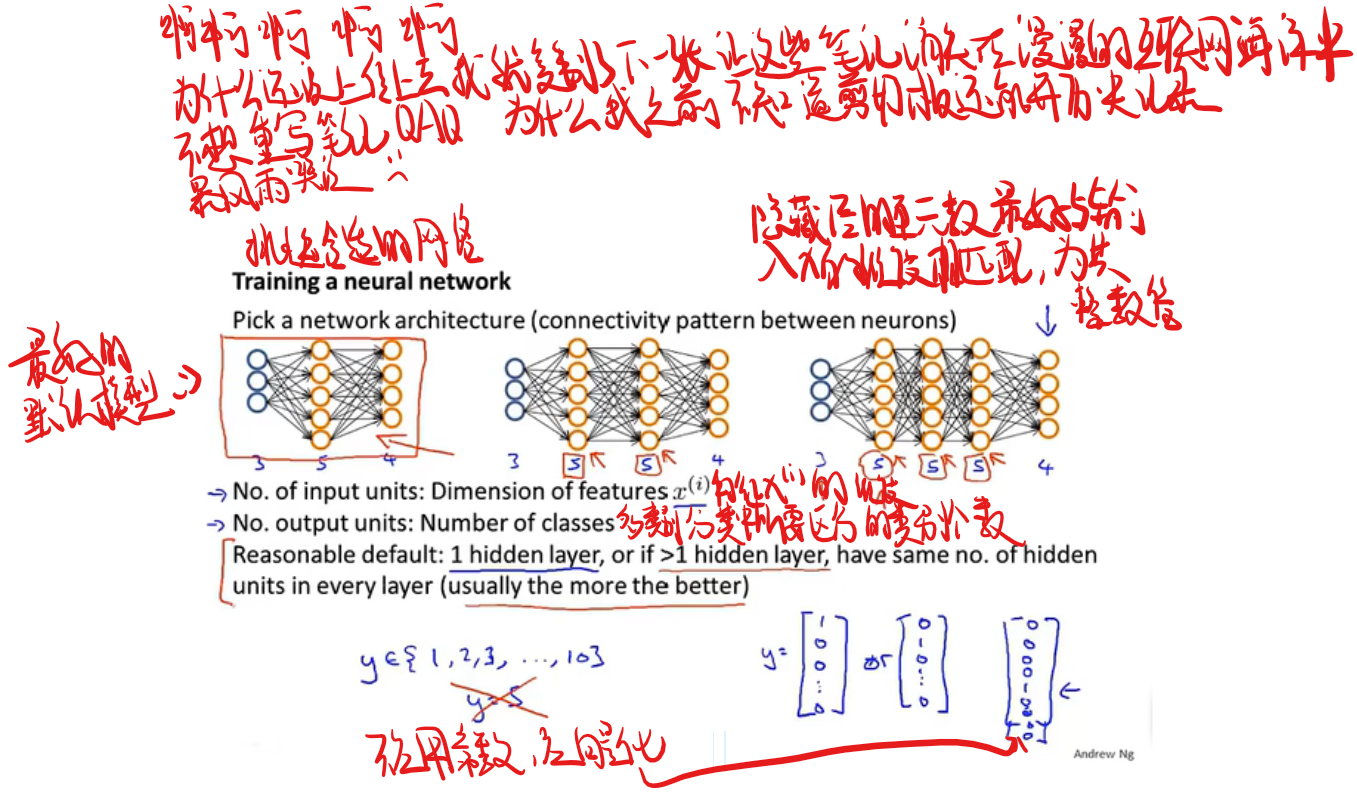
总结如何搞训练神经网络:
首先将权重随机初始化为一个接近0的范围在$-\epsilon$到$\epsilon$之间的数,然后进行反向传播,再进行梯度检验,最后使用梯度下降或者其他高级优化算法来最小化代价函数J($\theta$),整个过程从为参数选取一个随机初始化的值开始,随机初始化的选取过程是一个打破对称性的流程,随后通过梯度下降或者高级优化算法就能计算出$\theta$的最优值。
最终的总结


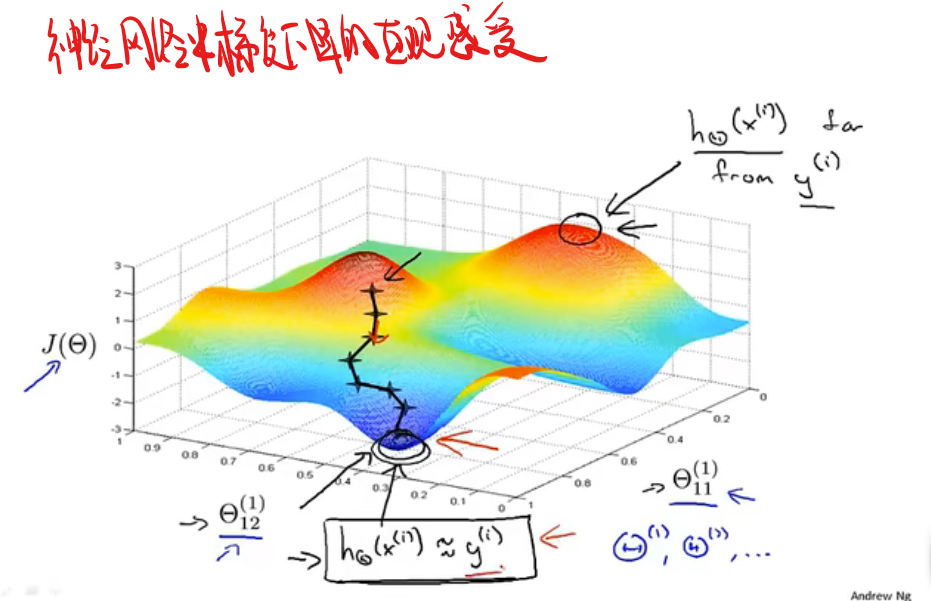
此处老师举了个无人驾驶的例子 1992年就实现了我焯 好牛
如何选择算法啥的
如何评估机器学习算法的性能
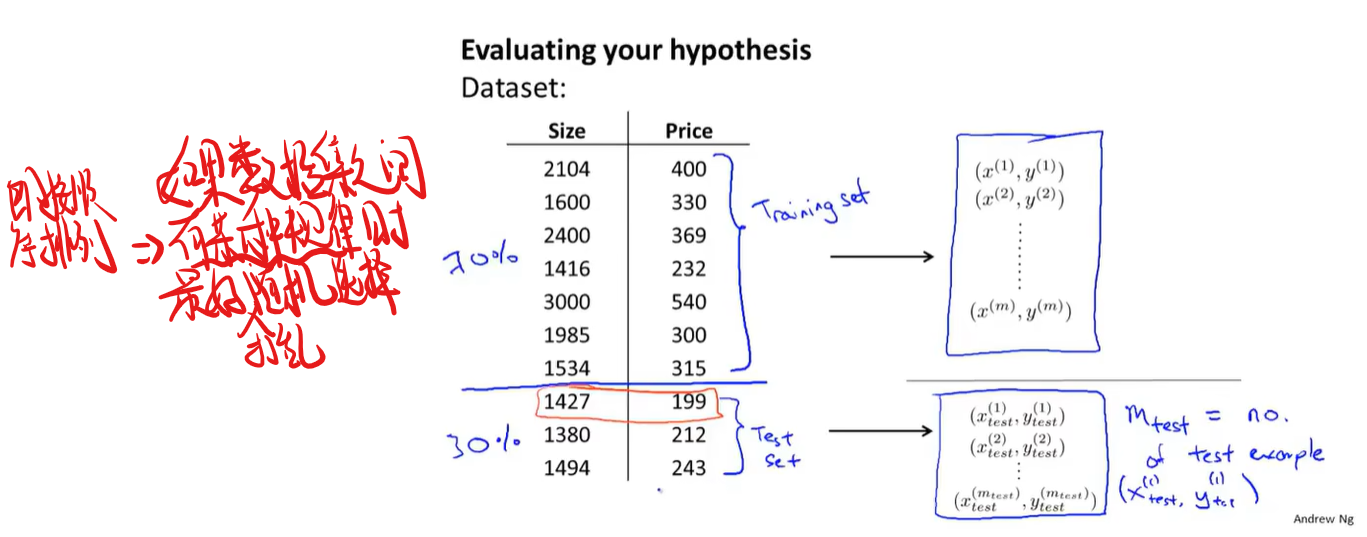




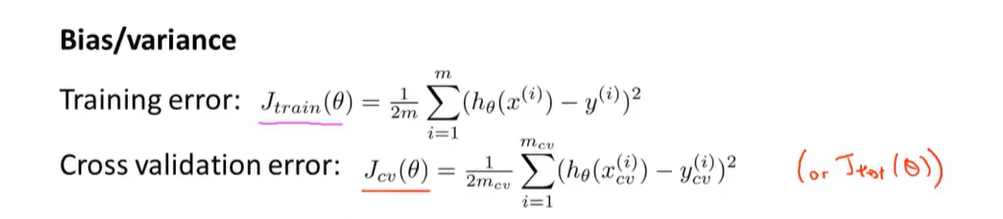
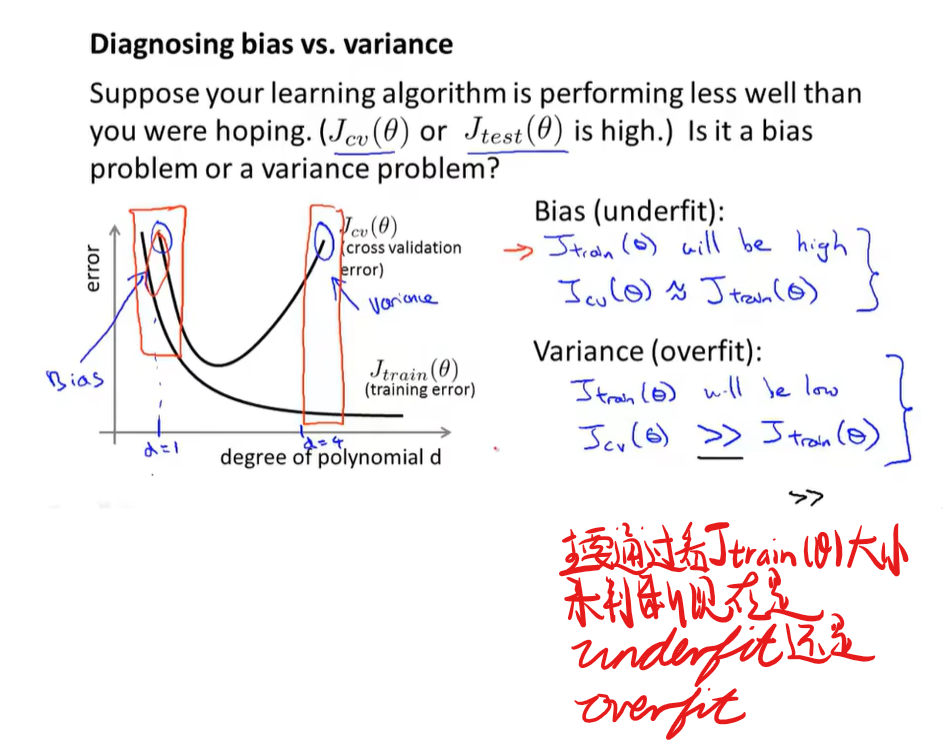
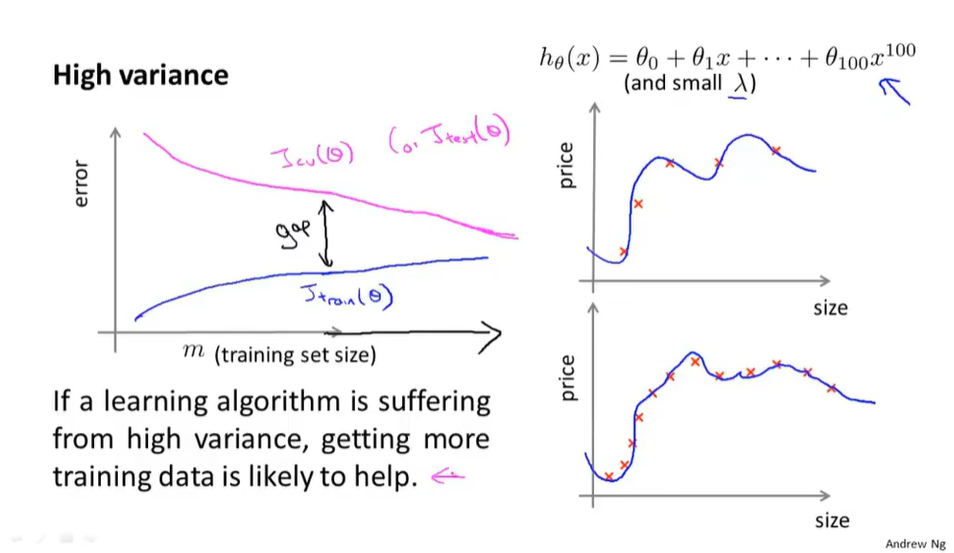
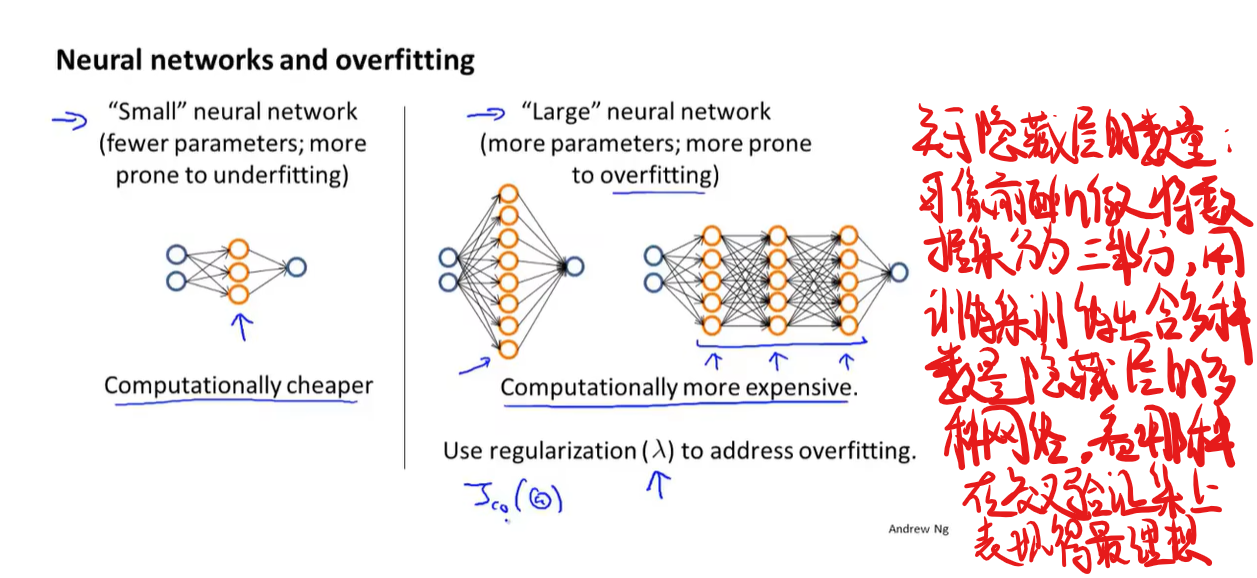
偏差和方差和正则化的关系
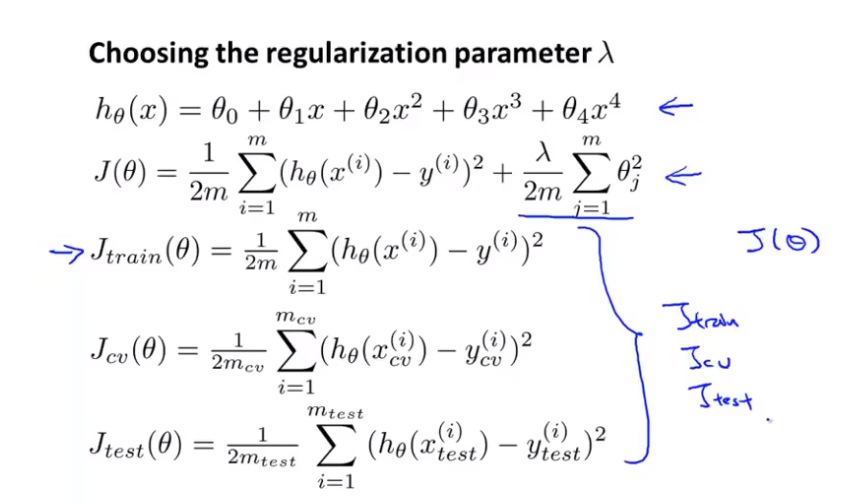

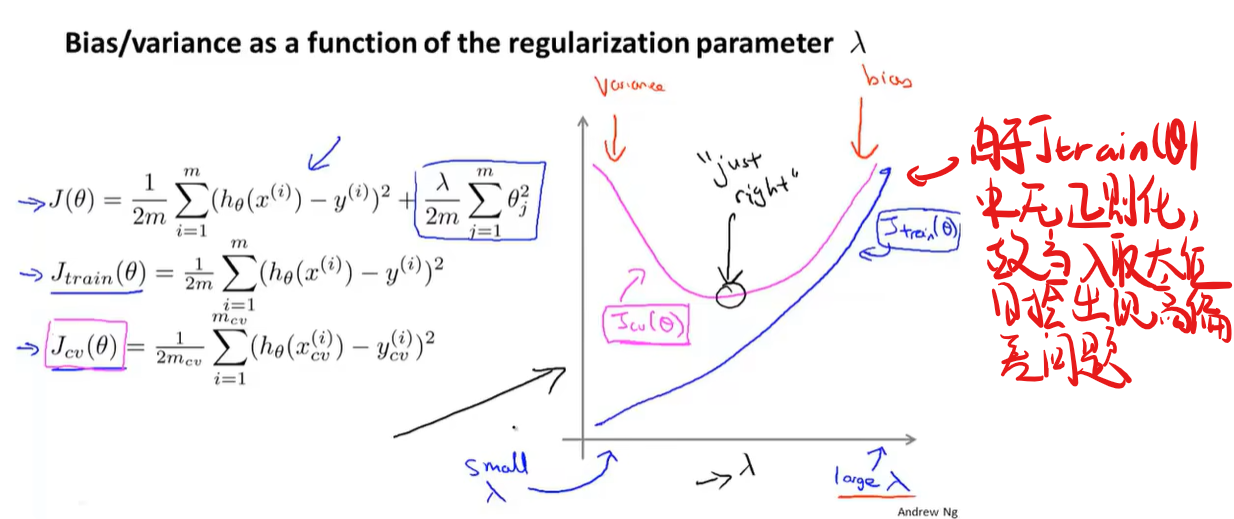
机器学习诊断法

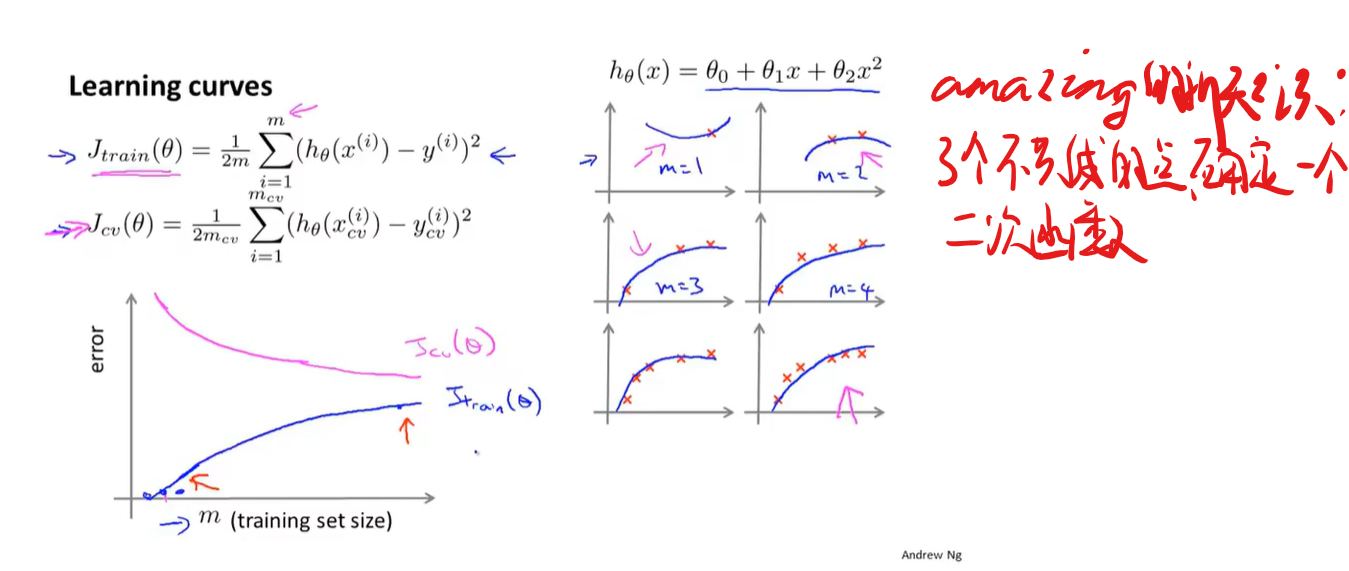
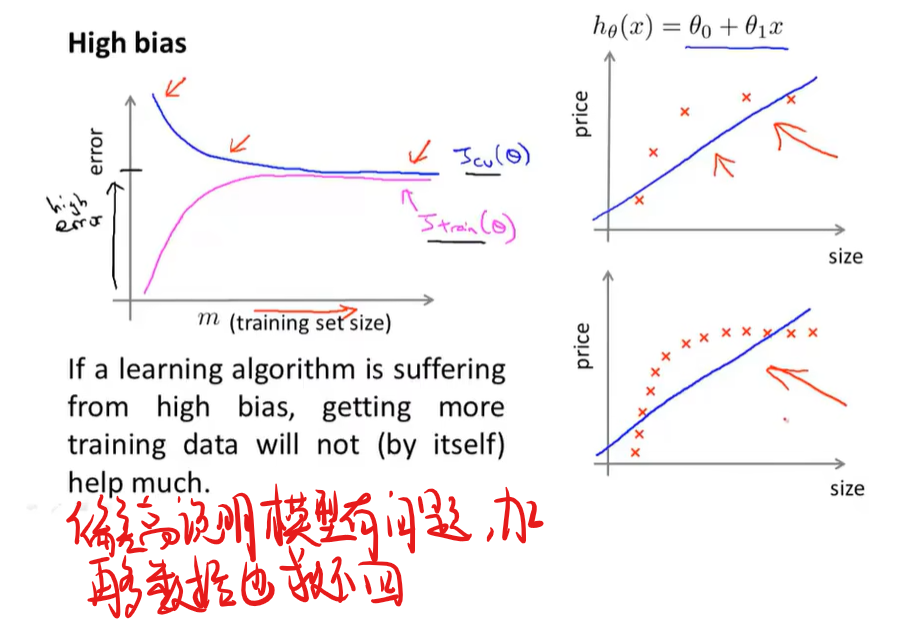

又开始夸大家超过大部分的硅谷工程师了,老师您在夸的时候能收敛一下脸上的谜之笑容吗
机器学习系统设计
误差分析
1.可以手动分析数据集,将交叉数据集分类并查看分类出来的邮件是否符合所设的特征,如果match了很少的特征则可以将这个特征砍掉
2.通过数值方法(numerical evaluation)来评估算法的效果
总之就是在犹豫一种算法时不如直接在交叉验证集上用单一规则的数值评价指标,观察误差率是变大了还是变小了来决定搞不搞,莽就完了
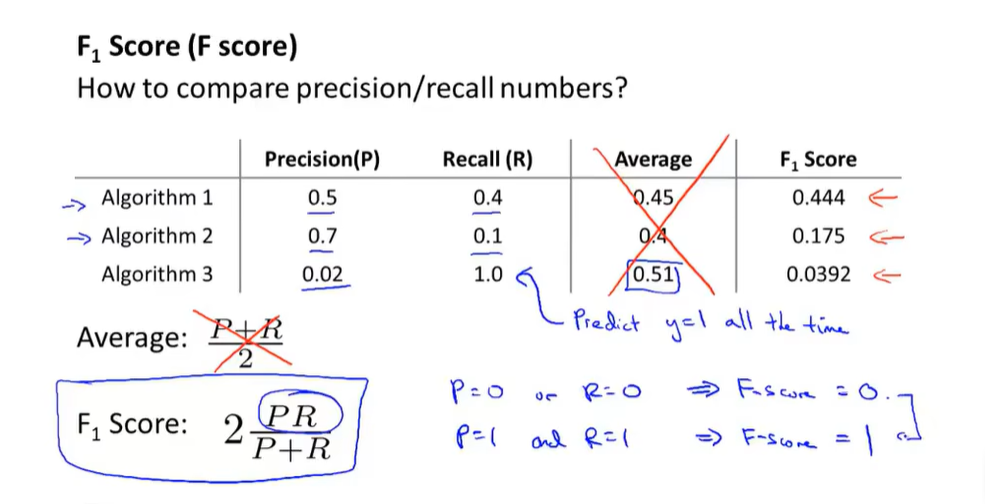
如何使用一个合适的误差度量值(偏斜类问题)



什么时候用更多数据可以解决问题
1.特征值x有充足的信息来确定y,eg.让电脑做完形填空
如何判定x是不是有充足的信息来确定y呢,可以假设让人类专家来答这个问题,一位英语专家显然能很好地做完形填空,故这种就是x有充足的信息来确定y;但一个金融专家显然不能很好地预测哪支股票哪支基金会涨(呜呜我的钱QAQ),这种就是x没有充足的信息来确定y
2.用一个超级无敌复杂的模型时也可以用很多的数据
省流:特征超多或模型超复杂时用更多的数据来喂饱这个模型吧!
支持向量机(SVM)
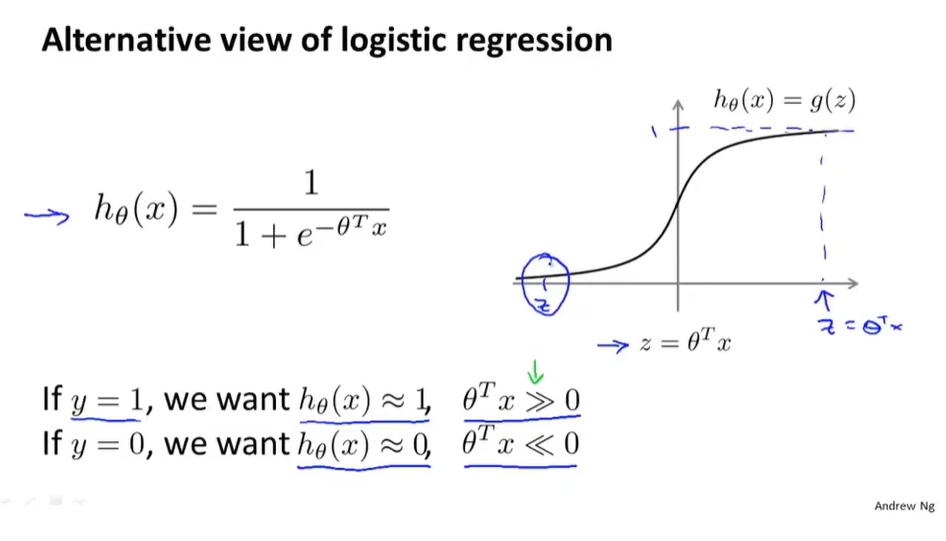

图中$A+\lambda B$与$CA+B$中的$\lambda$与$C$均为给B和A设权重,来决定我们是更关心第一项的优化还是更关心第二项的优化(C<1)
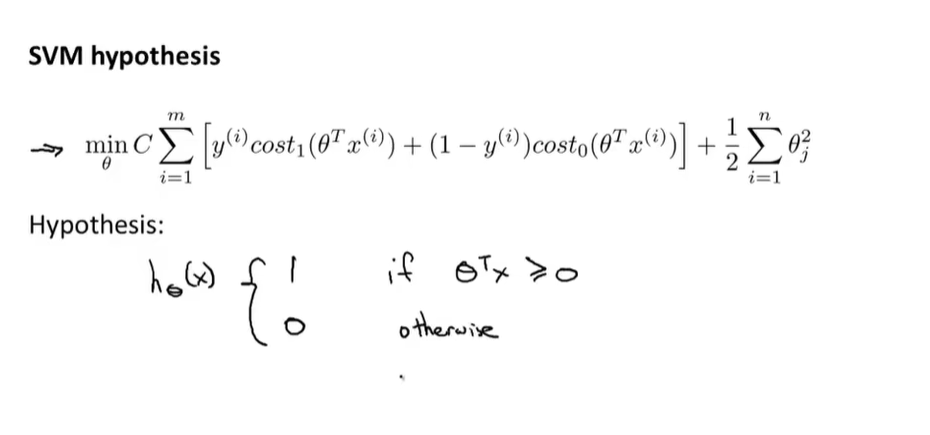
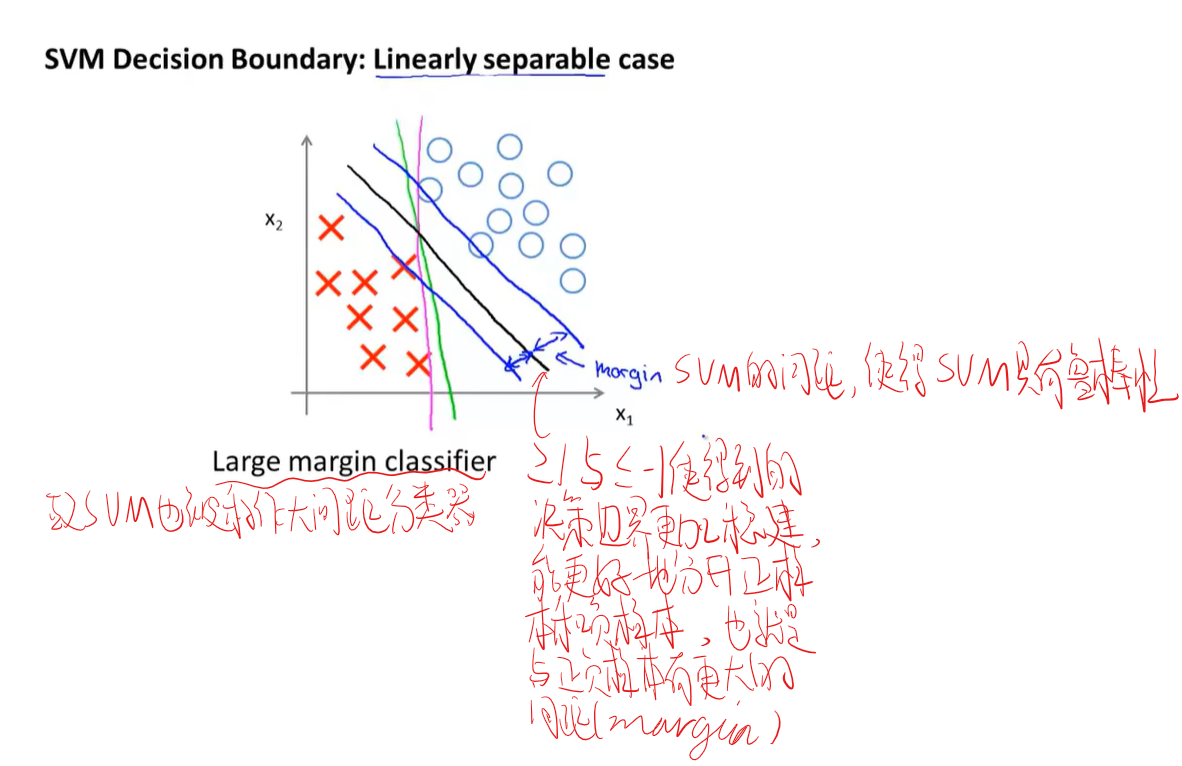
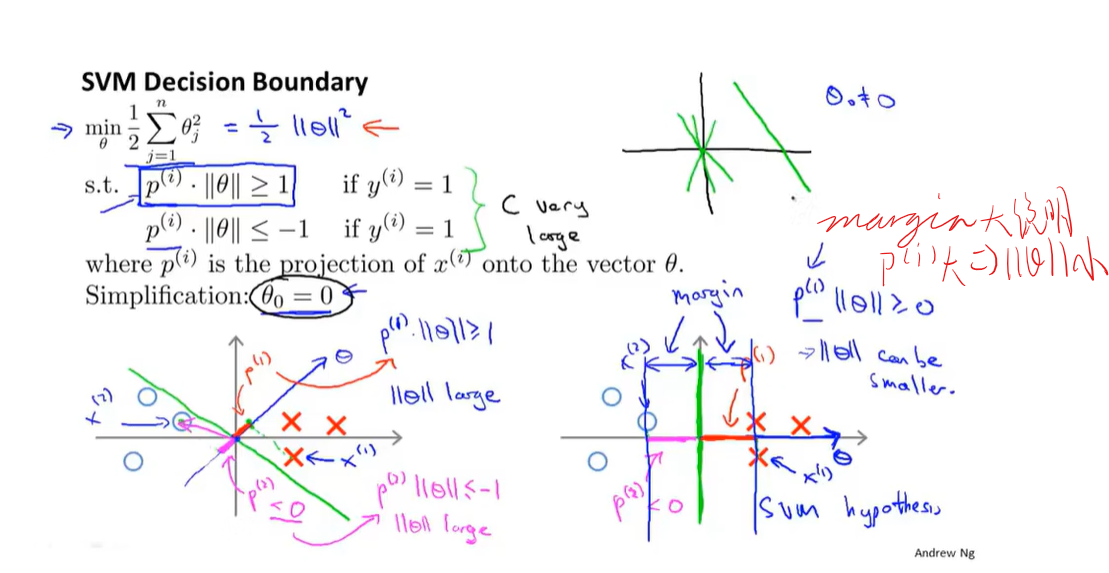
为什么支持向量机又称大间隔分类器

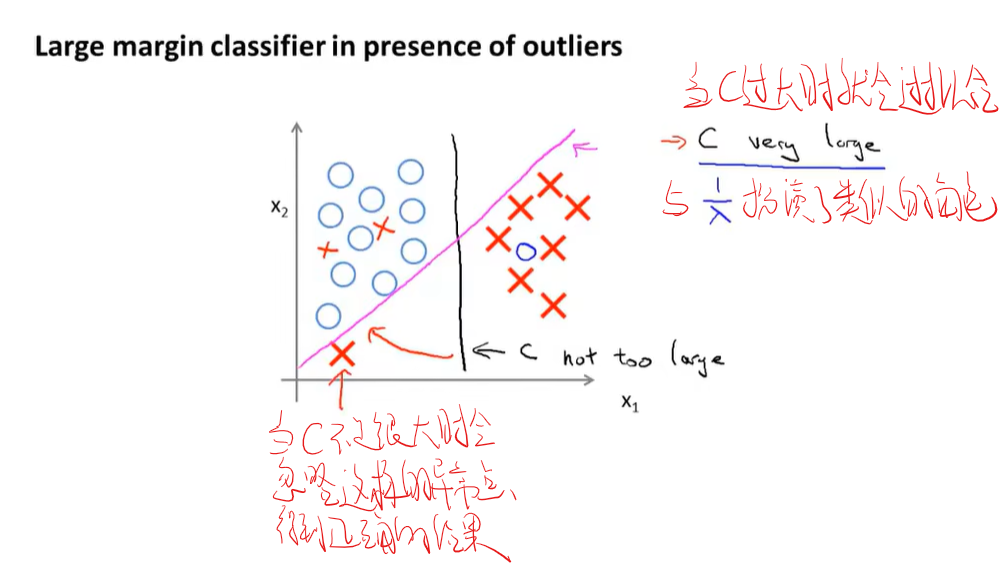
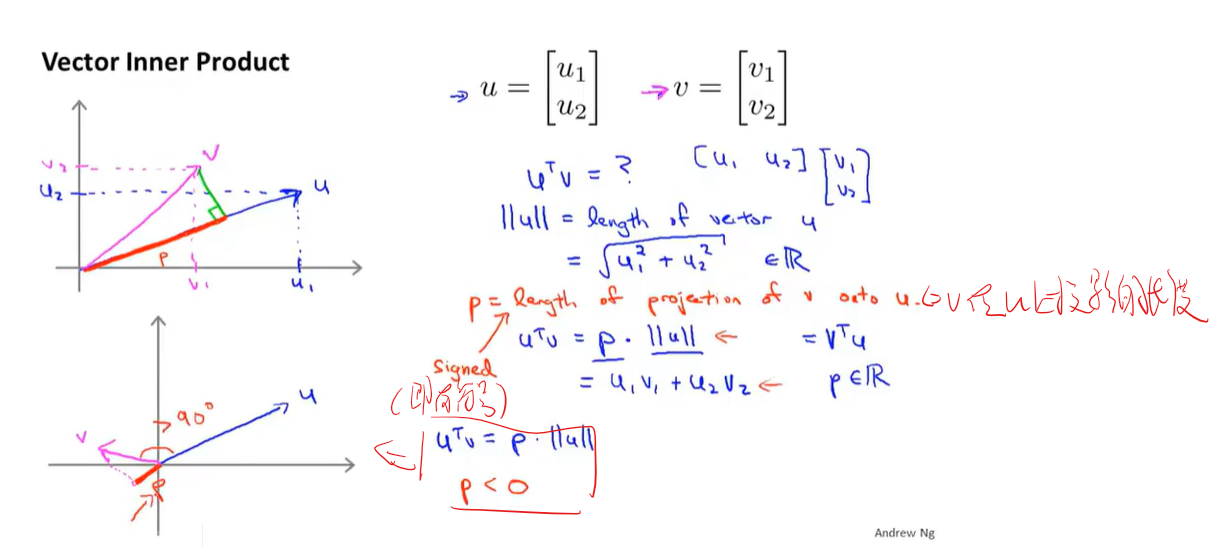
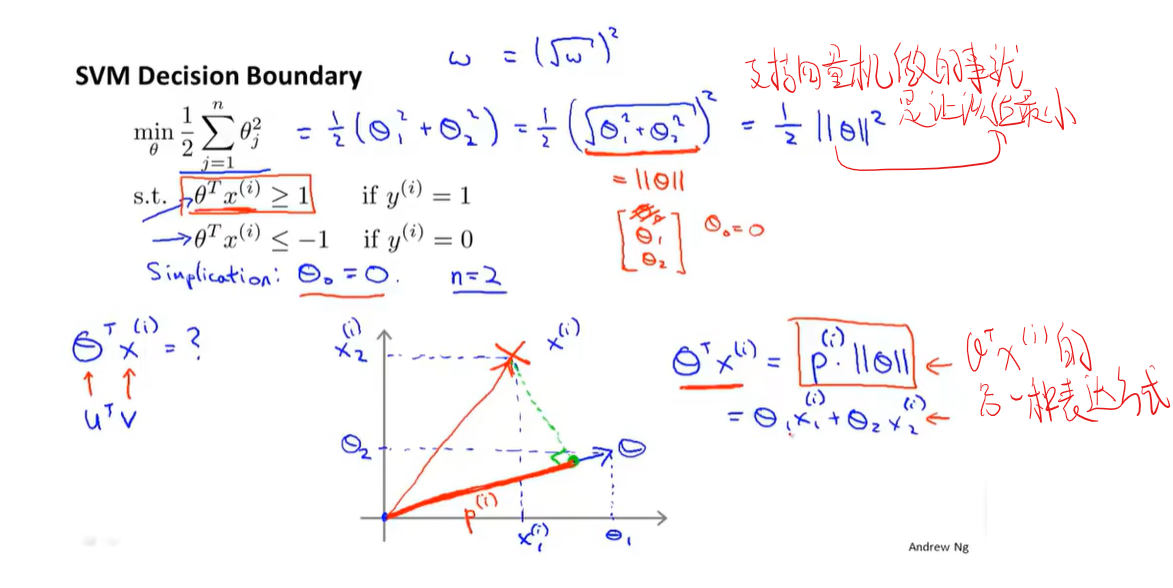
支持向量机的数学原理
核函数


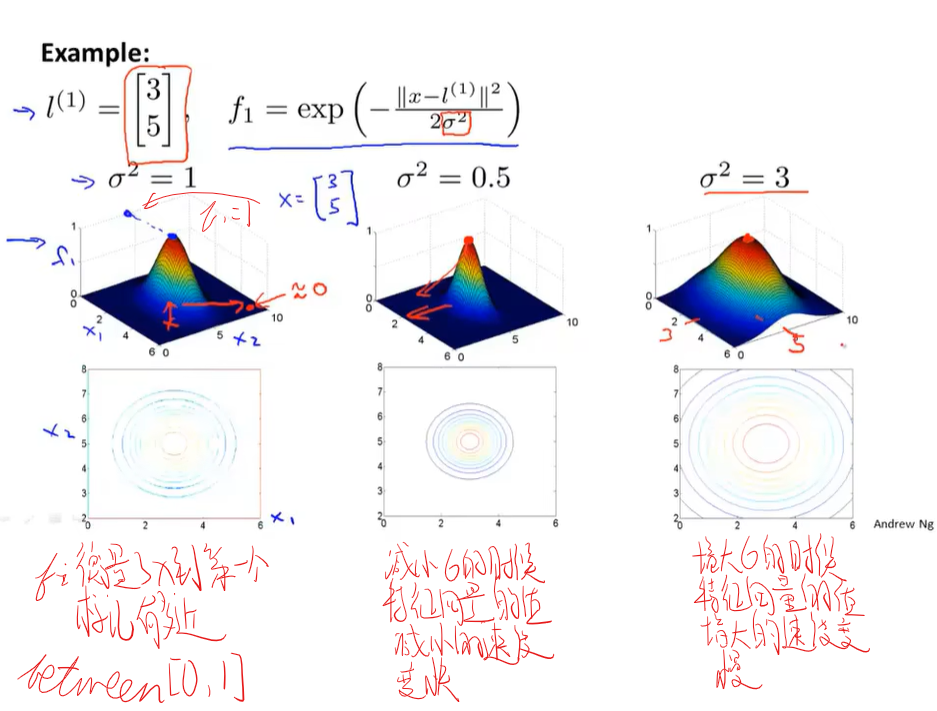

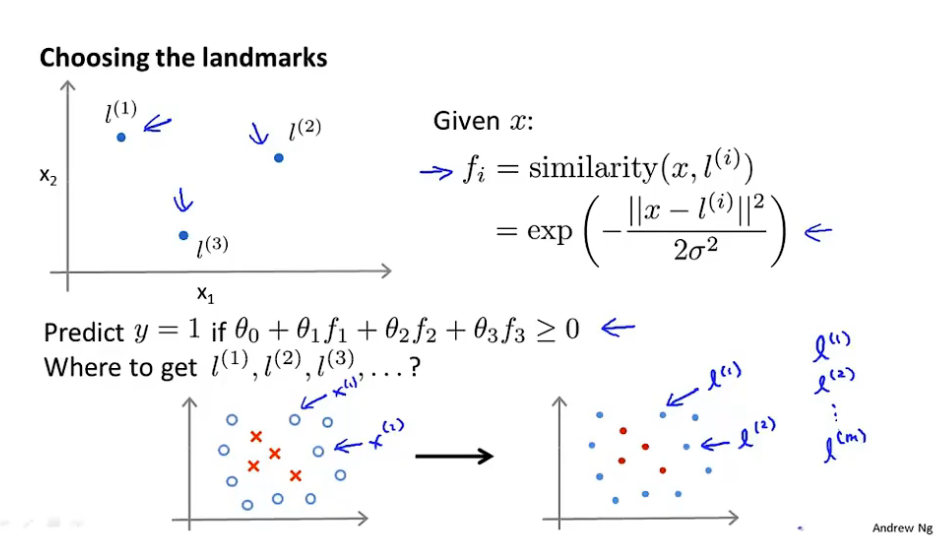



使用SVM





无监督学习
大致定义
给予机器没有标准答案的数据让机器自己分类找出数据的结构,eg.聚类算法,鸡尾酒会算法
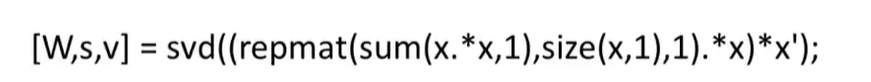
据说这样一行就可以了 amazing
好吧 是在octave里
K-Means算法
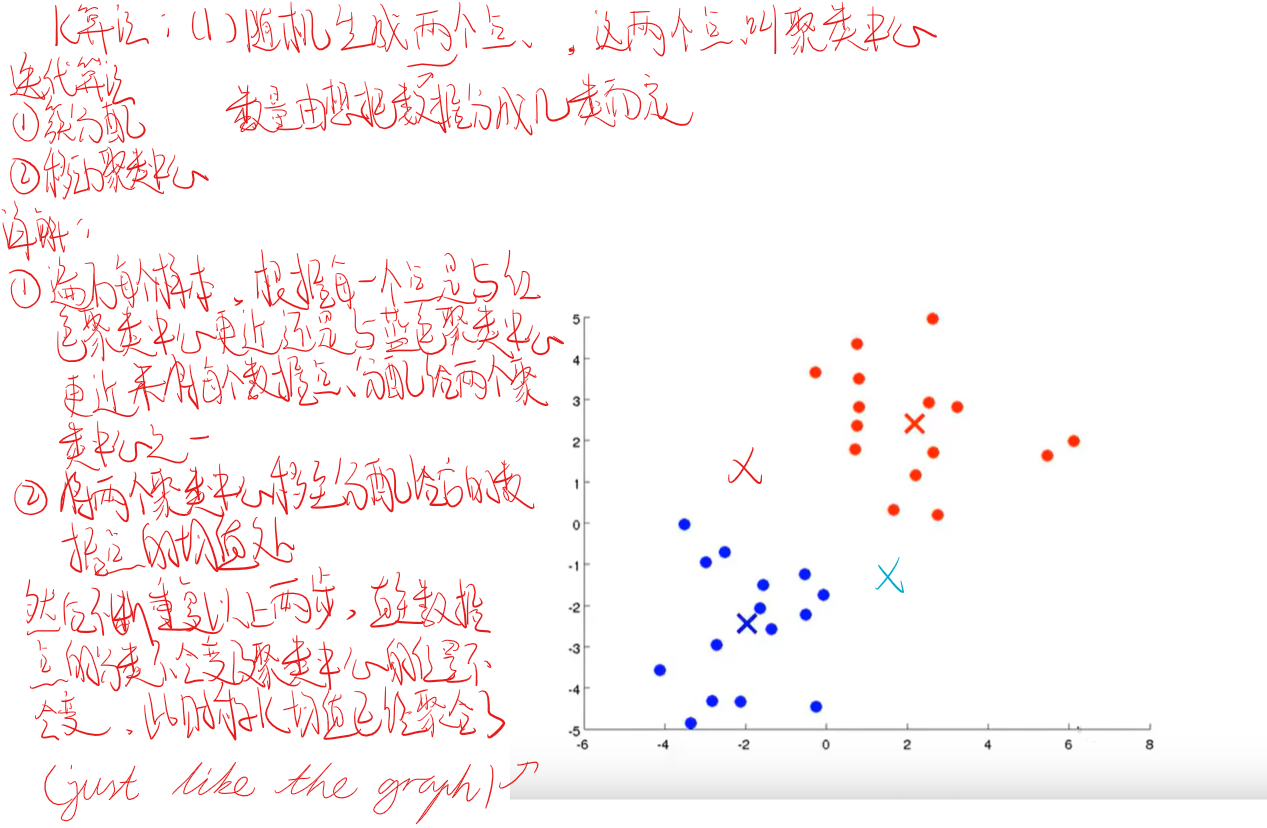


代价函数



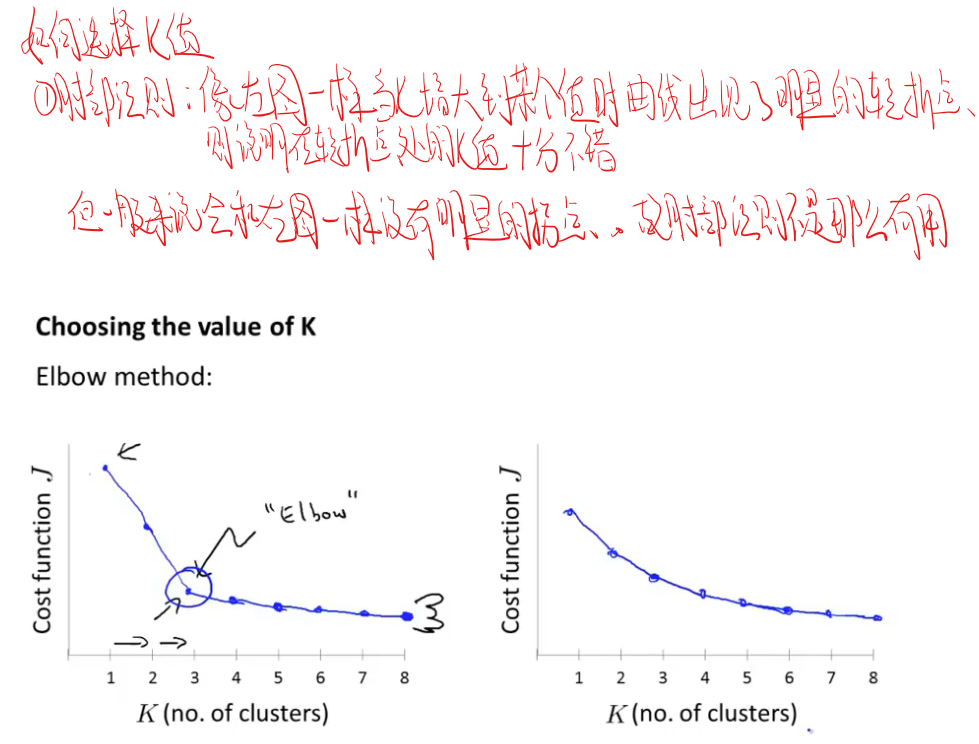
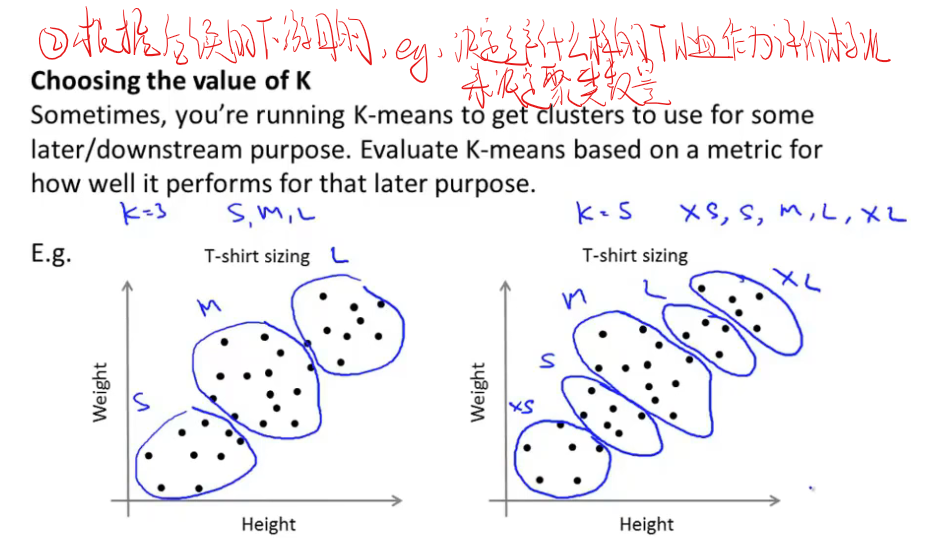
如何选择K值(聚类数量)
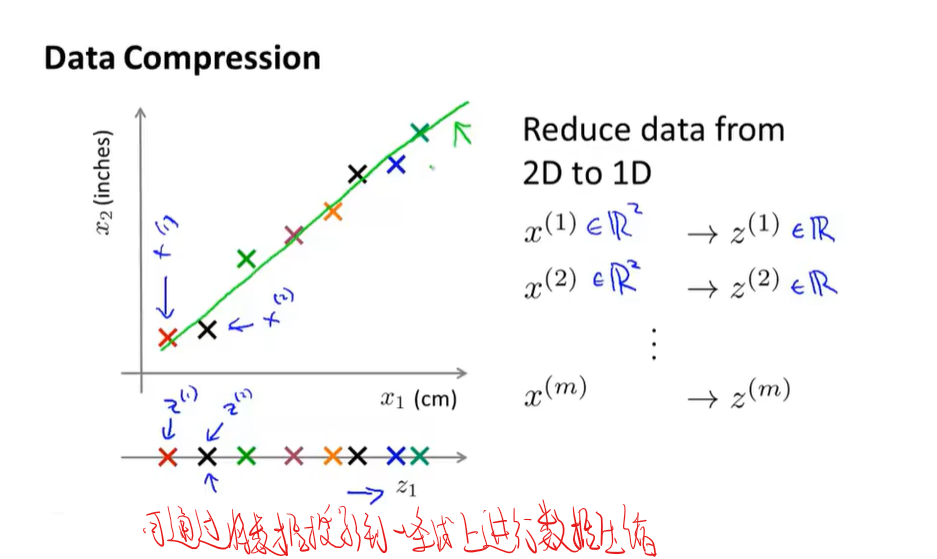
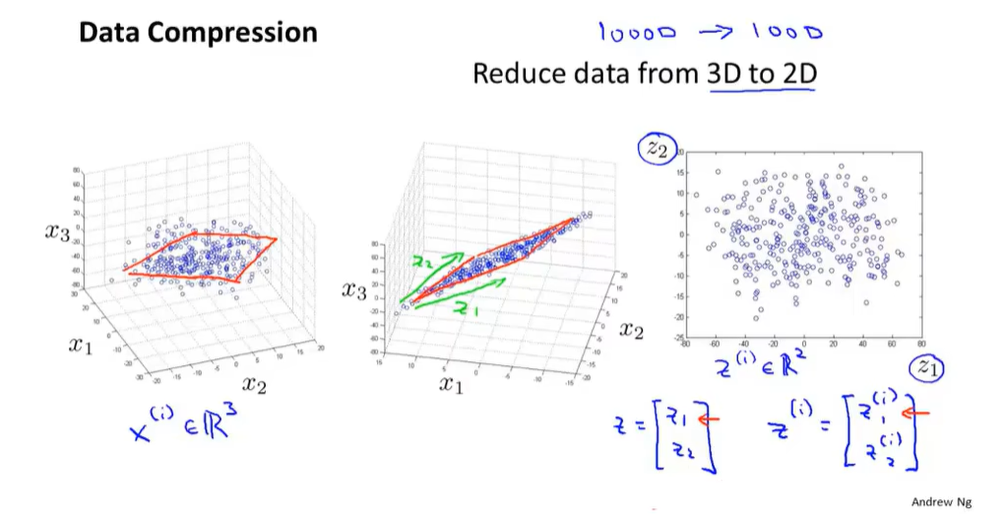
降维(PCA)
删除高度冗余的特征
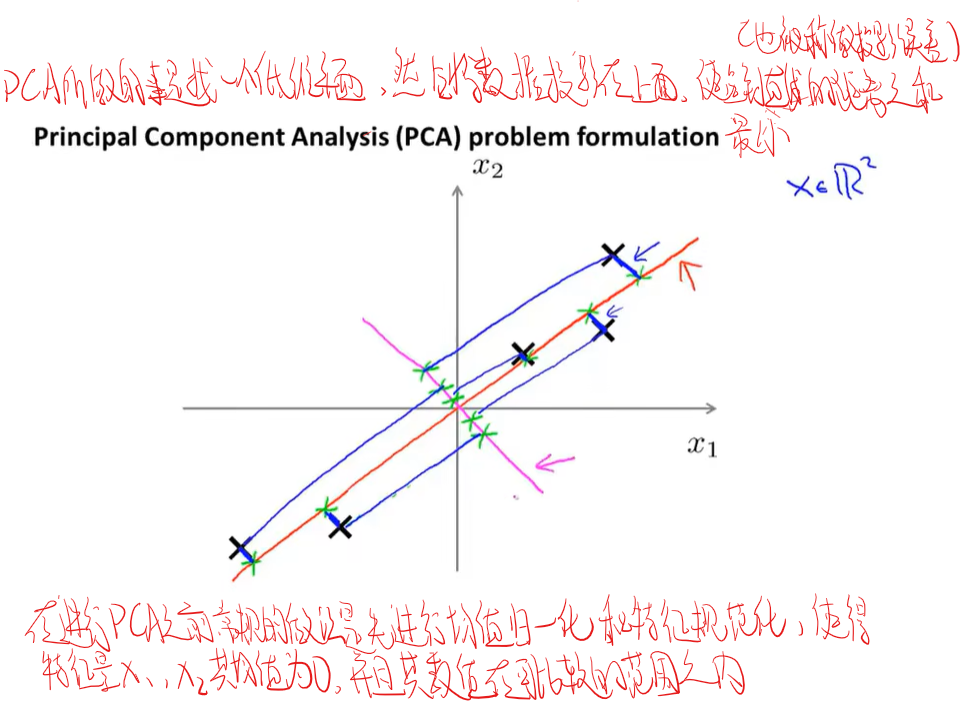
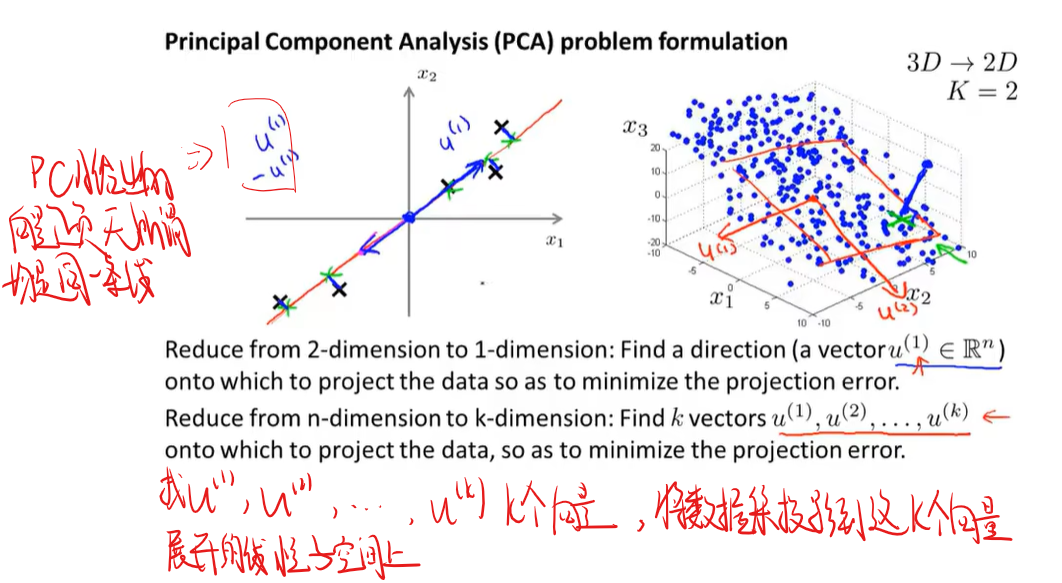
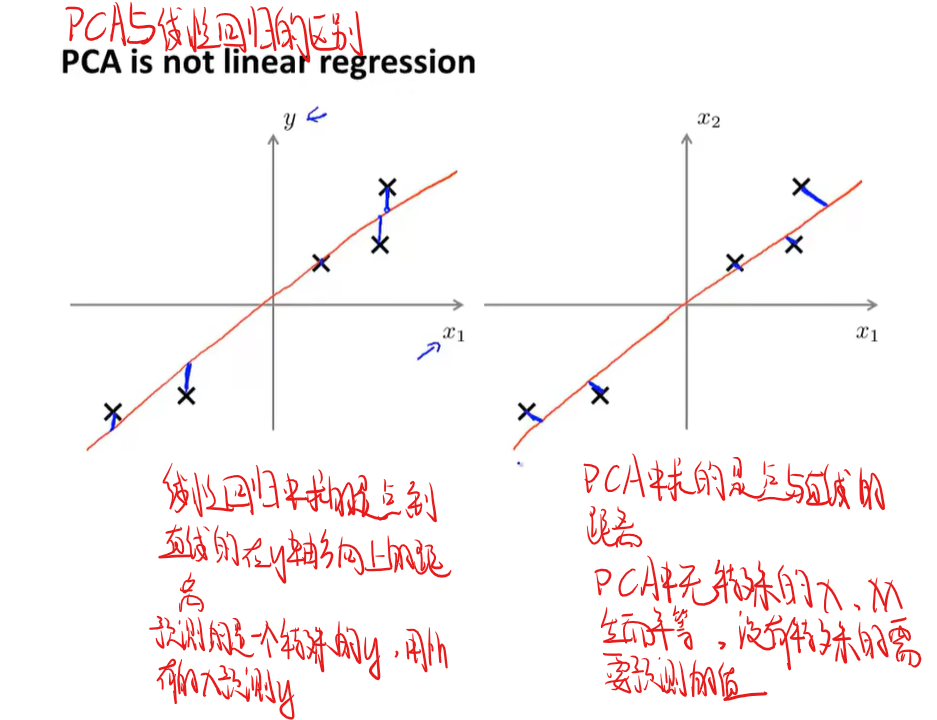


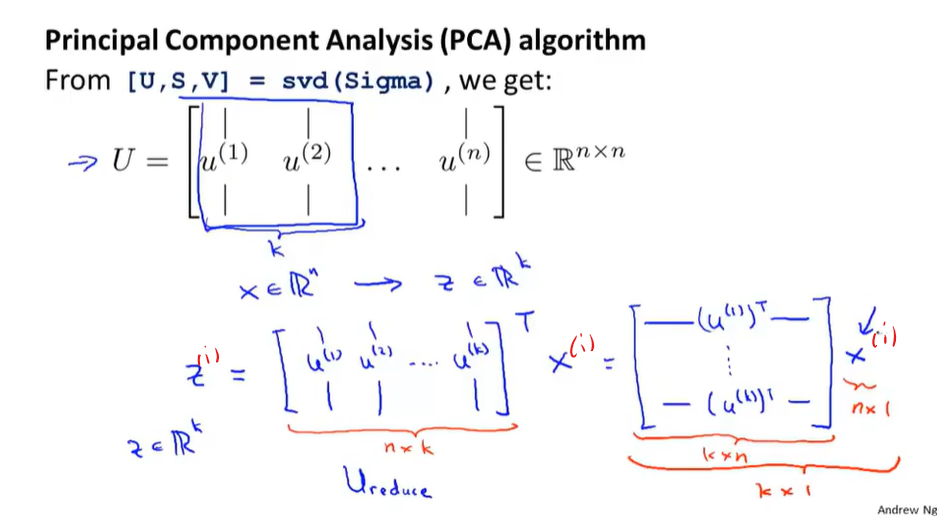

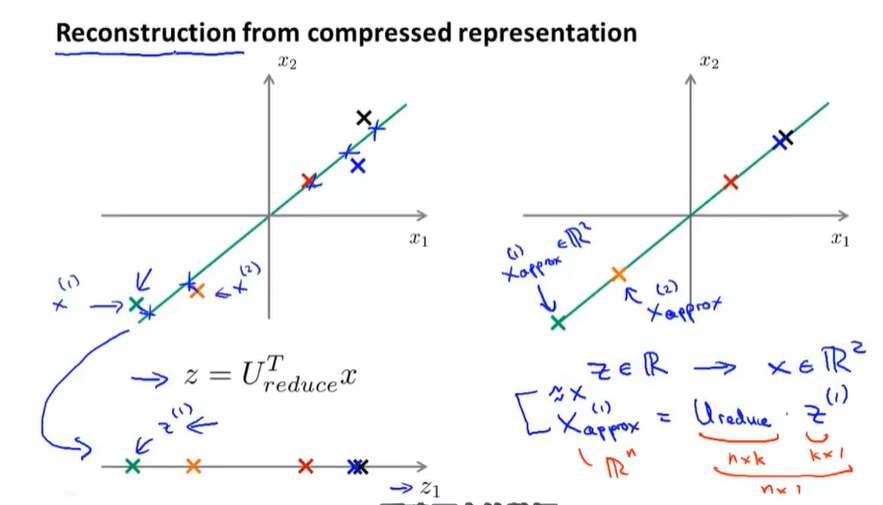
如何将PCA后得到的低维数据还原成高维数据
如何选择k


应用PCA的建议



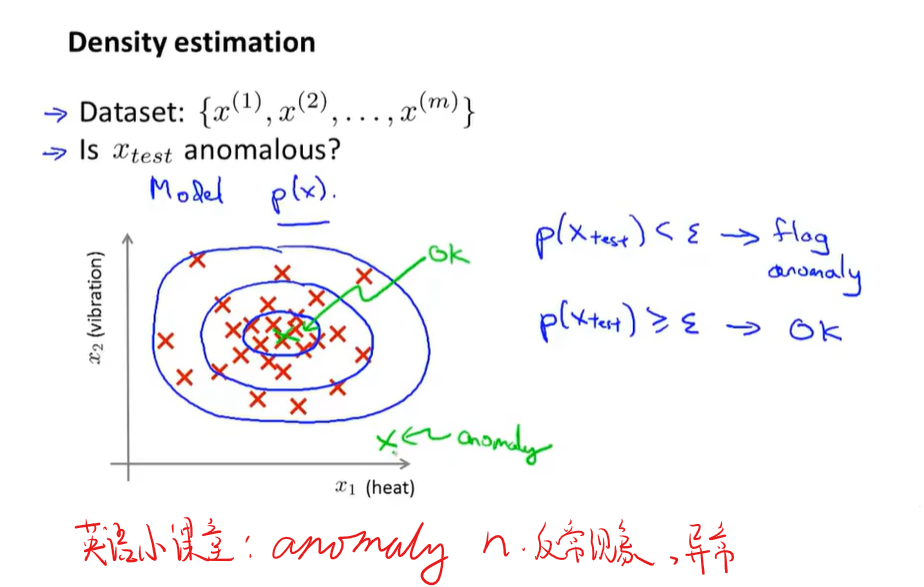
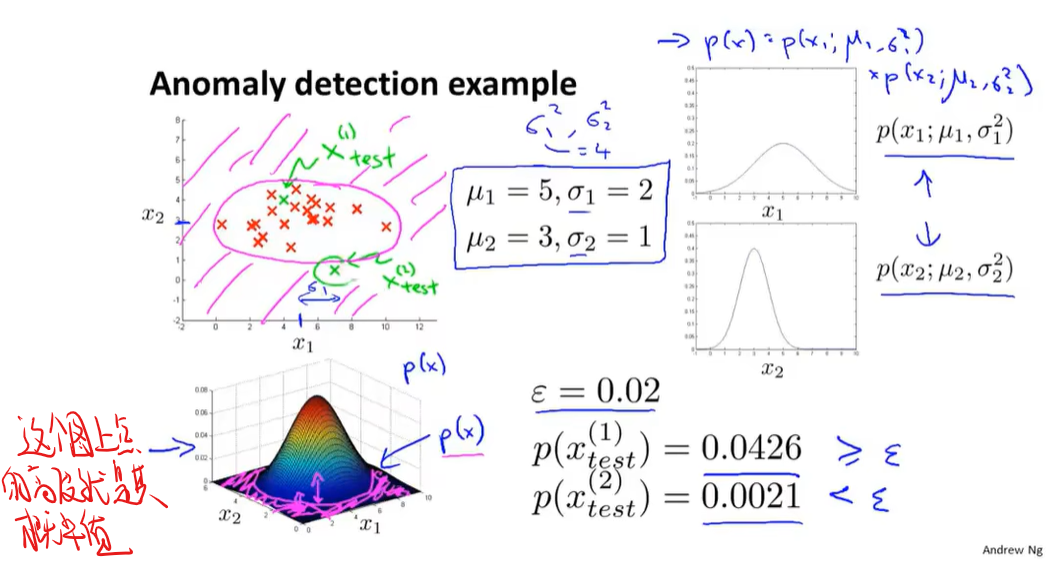
异常检测